

Aula 1:
Introdução à disciplina de Controle Digital
SEL0359
Prof. Marcos Rogério Fernandes
8 de agosto de 2024
Objetivos
Os objetivos dessa aula são:
- Apresentar a disciplina: estrutura e métodos de avaliação;
- Visão Geral dos conceitos de sistemas de controle;
- Apresentar exemplos práticos de sistemas de controle digital;
- Comparativo entre controle analógico e digital;
- Evidenciar a importância dos sistemas de controle digitais para a engenharia;
SEL0359 - Controle Digital
Encontros:
- quintas-feiras às 14h20-16h00 => aula teórica (D02)
- sextas-feiras às 14h20-16h00 => aula prática (laboratório G1-STI)
Contato: marofe@usp.br
Tópicos
- Representação de sistemas em tempo discreto;
- Amostragem de sinais;
- Transformada Z e discretização de sistemas;
- Análise de estabilidade em tempo discreto;
- Projeto de controladores PID discreto;
- Modelos em Espaço de estados à tempo discreto;
- Projeto de controle via realimentação de estados;
- Projeto de observadores de estado;
- Controle LQR e Filtro de Kalman.
Material da disciplina

- Slides;
- Notas de aula;
- Listas de exercícios;
- Vídeos relacionados aos tópicos;
- Códigos, exemplos ilustrativos, etc...
Material da disciplina
Referências
- [1] Bruno A. Angélico and Gabriel P. Das Neves. Controle Digital Aplicado. Editora Blucher, 2023.
- [2] E. M. HEMERLY. Controle por Computador de Sistemas Dinâmicos. Editora Blucher, 2nd edition, 2000.
- [3] Katsuhiko Ogata. Discrete-Time Control Systems. Prentice Hall, 2nd edition, 1995.
Avaliação
Serão realizadas:
- Duas provas teóricas: $P_1$ e $P_2$;
- Uma prova prática $P_1^{LAB}$ (Matlab);
- Listas de exercícios computacionais $L_1,\ldots,L_n$;
- Ao final do semestre, um trabalho computacional $T$.
Avaliação
A média final é dada por:$$MF=0.5P+0.3L+0.2T$$
$$P=mean(P_1,P_2,P_1^{LAB})$$ $$L=mean(L_1,L_2,\ldots,L_n)$$
Avaliação
Para aprovação, é necessário:
- Ao menos $70\%$ de frequência, $P\ge 4.0$ e $MF\ge5.0$;
- Se $3.0\le P < 4.0$, aluno ficará de recuperação independente da $MF$;
- Se $P<3.0$ mas $MF\ge 3.0$ então aluno poderá fazer recuperação;
- Se $MF<3.0$ ou menos $70\%$ de frequência o aluno é reprovado.
Dúvidas?

Introdução
O que é um sistema de controle?
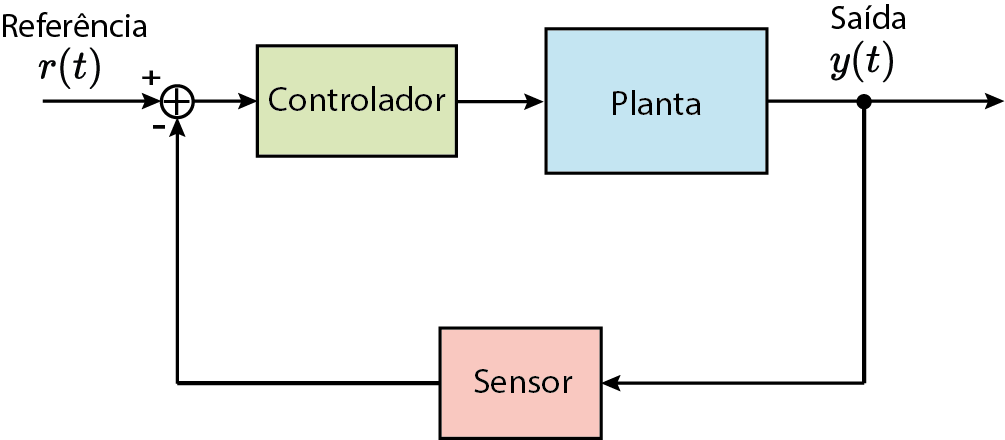
Garantir desempenho e segurança!
História

História
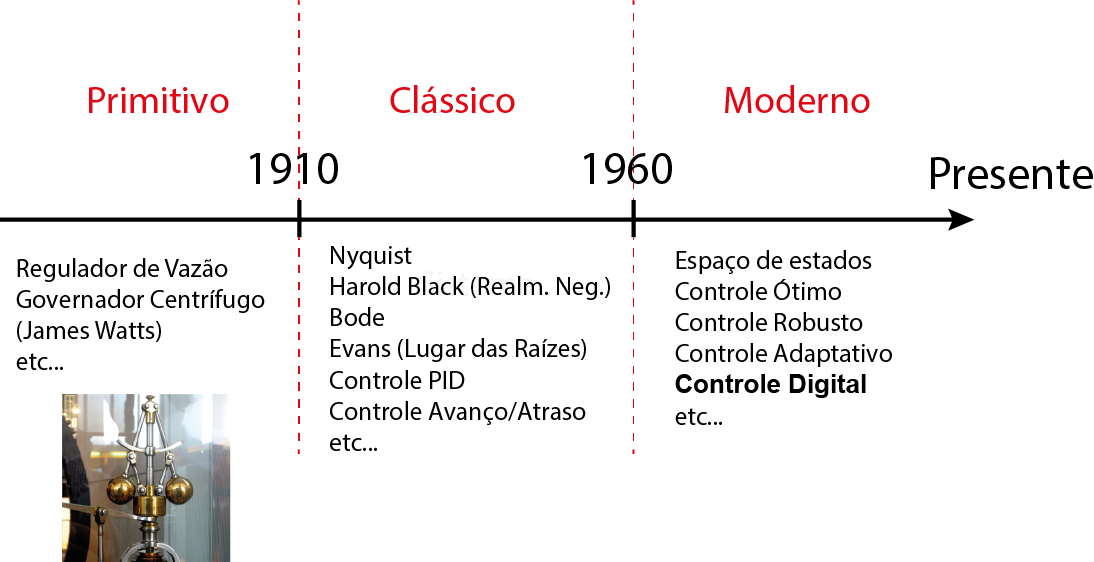
História
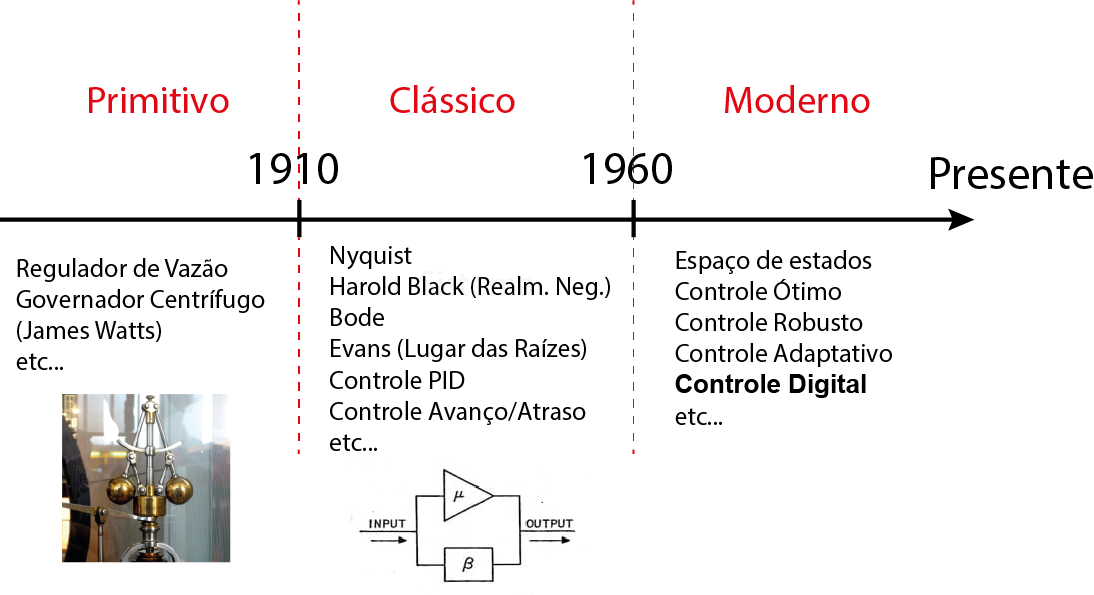
História
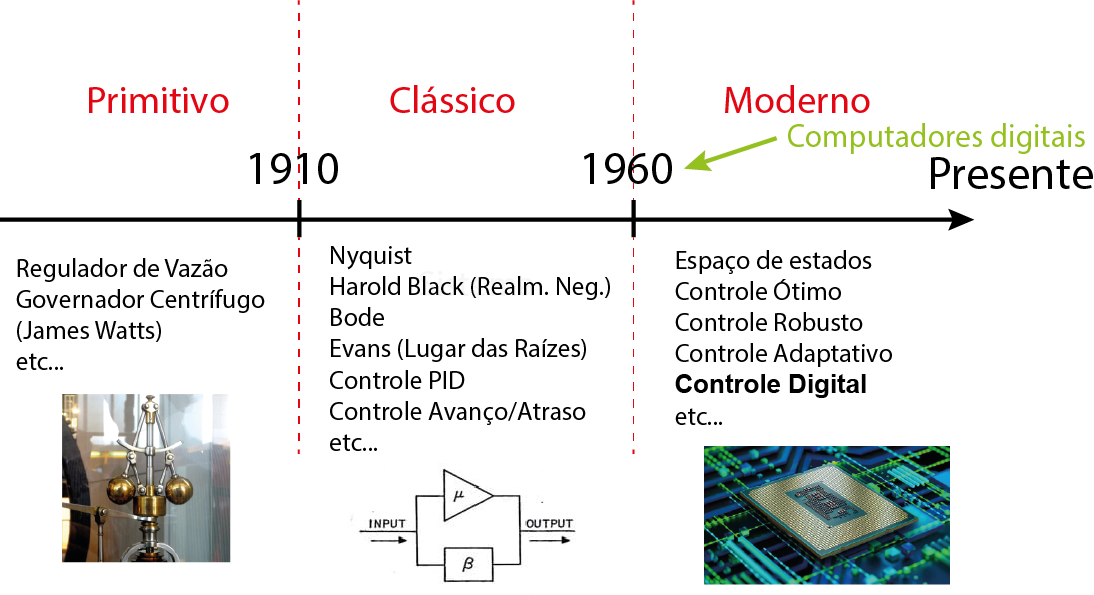
Exemplos
Naves espaciais e aviões
 |  |
Ex: controle de atitude
Rocket Landing System
Geração de energia
 |  |
Ex: controle de potência gerada
Indústria
 |  |
Ex: controle de temperatura, vazão, nível...
Setor automotivo
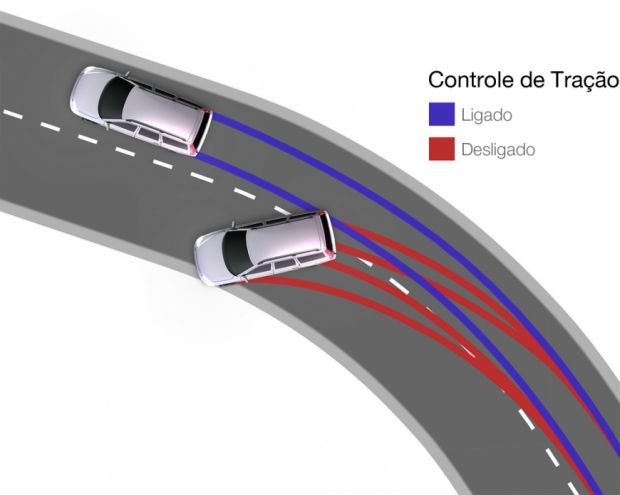 Fonte: https://salaodocarro.com.br/como-funciona/controle-de-tracao.html |  |
Medicina (Ex: Controle de Diabetes)
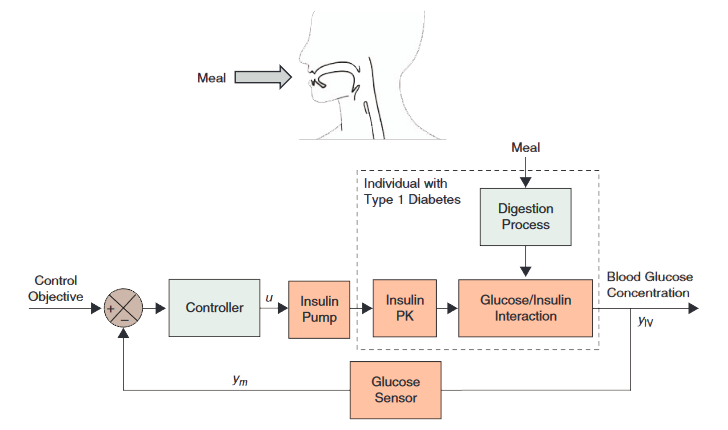
Biologia (Ex: Controle de Populações)
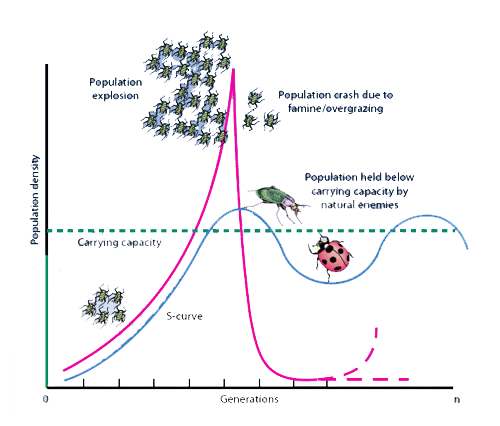
Tomada de decisão no Mercado financeiro e Economia
Sistemas de controle
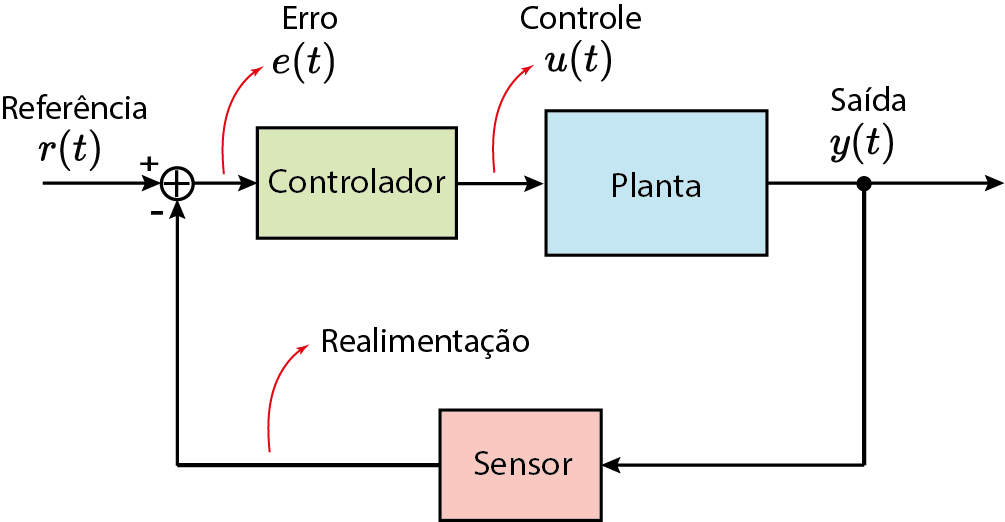
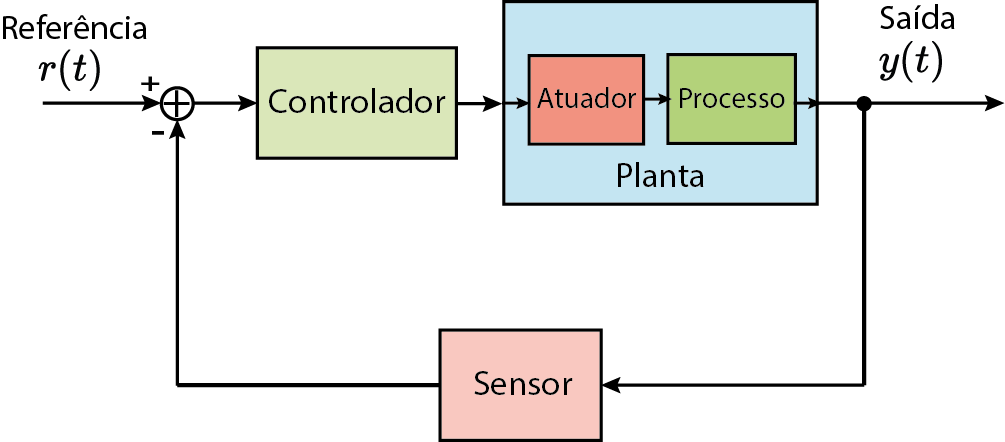
Processo pode ser físico ou não-físico.
Exemplos
Pêndulo Invertido:
https://www.youtube.com/watch?v=4kIrcELC79o
Pêndulo Invertido:
https://www.youtube.com/watch?v=4kIrcELC79o

Pêndulo Invertido:
https://www.youtube.com/watch?v=4kIrcELC79o
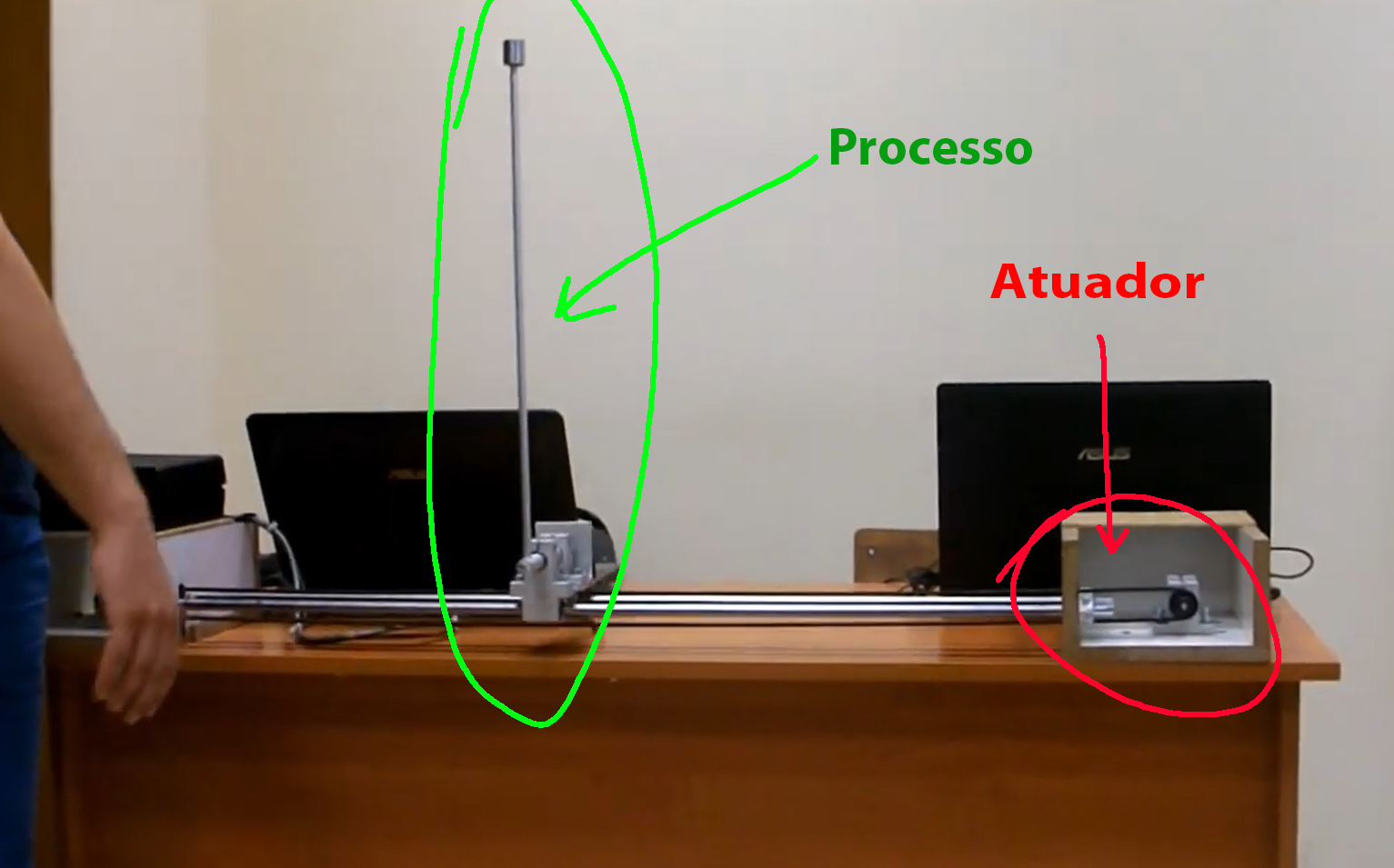
Pêndulo Invertido:
https://www.youtube.com/watch?v=4kIrcELC79o
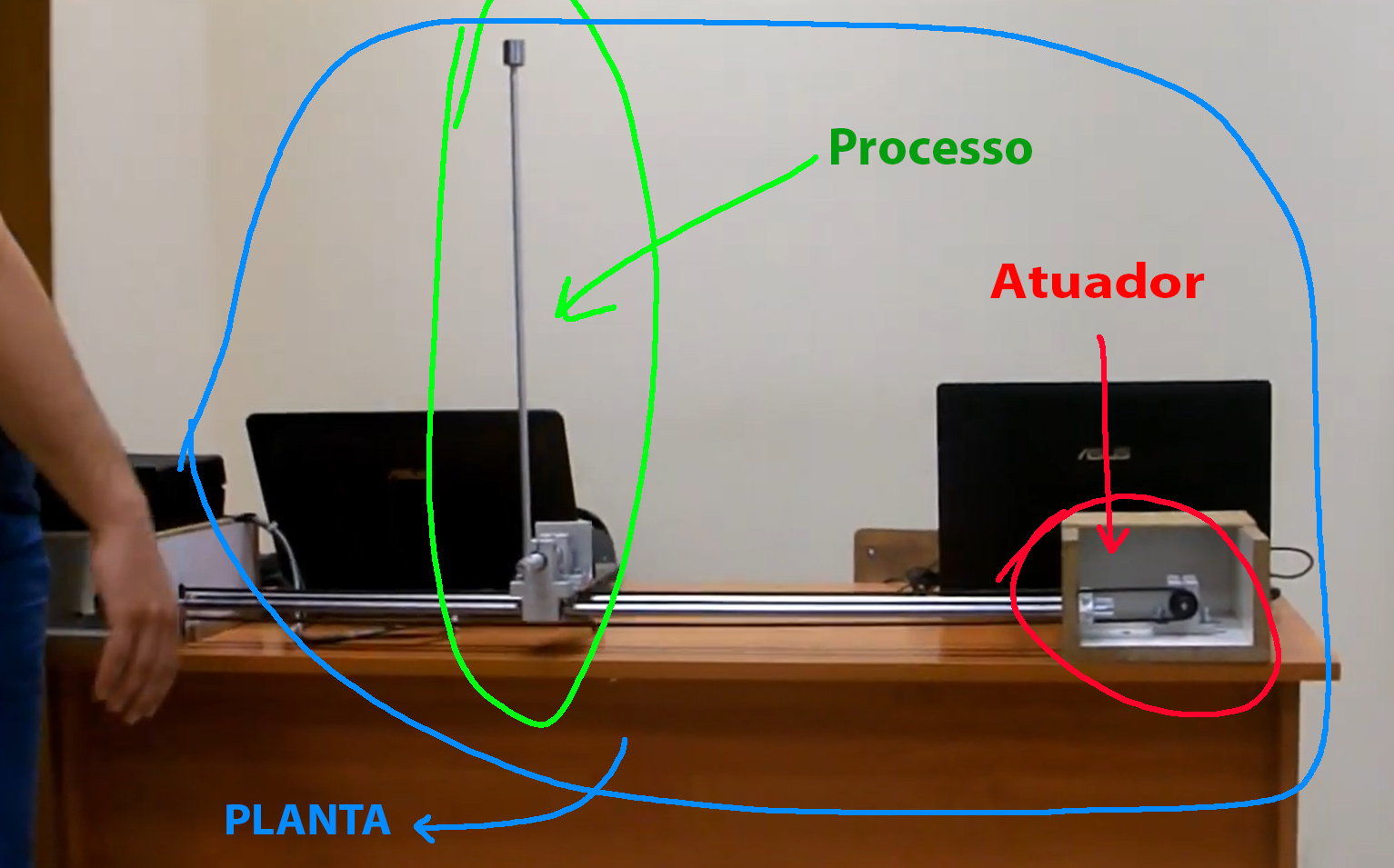
Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc
Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc

Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc

Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc

Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc

Self-balanced robot:
https://www.youtube.com/watch?v=38KVxZnBDZc

Requisítos
Um sistema de controle deve:
- Ser estável;
- Ser eficiênte (tempo de súbida, acomodação, sobresinal, etc):
- Rejeitar pertubações no processo;
- Ter robustez (ex: margens de ganho e fase);
Ciclo do Projeto de Controle
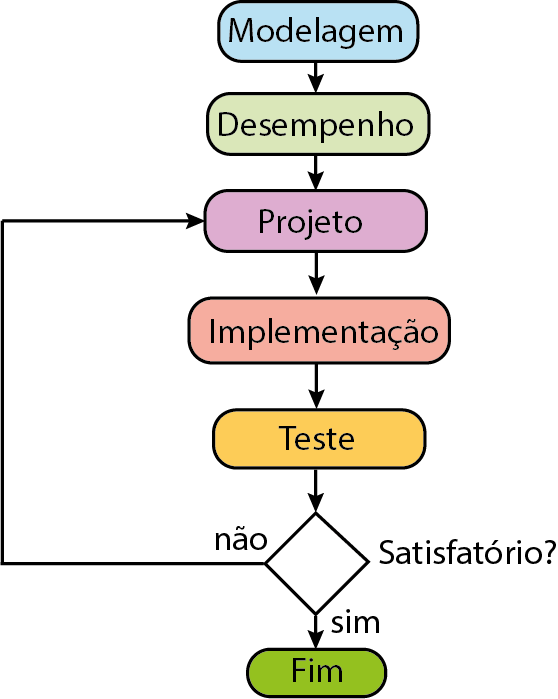
Ciclo do Projeto de Controle
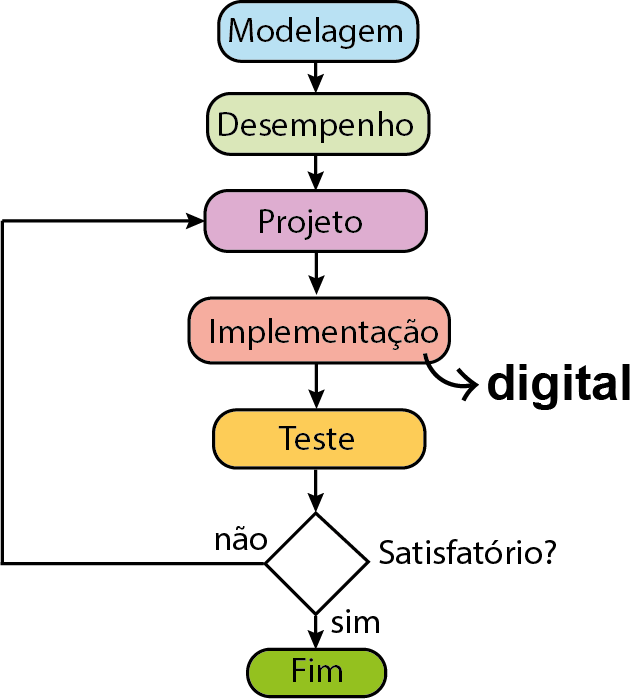
Modelagem
Obter Equações Diferênciais que descrevam a planta:
$$\sum_{n=0}^N \alpha_n\frac{d^n y}{dt^n}=\sum_{m=0}^M \beta_m\frac{d^m u}{dt^m}$$
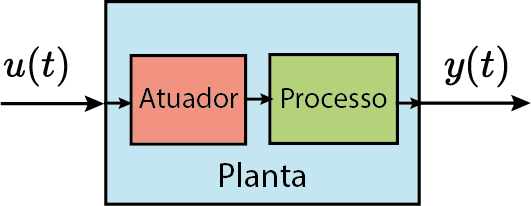
Modelagem
Obter Equações Diferênciais que descrevam a planta:
$$\sum_{n=0}^N \alpha_n\frac{d^n y}{dt^n}=\sum_{m=0}^M \beta_m\frac{d^m u}{dt^m}$$
- Abordagens em frequência: Função de Transferência
- Abordagens domínio do tempo: Espaço de estados
Critérios de Desempenho
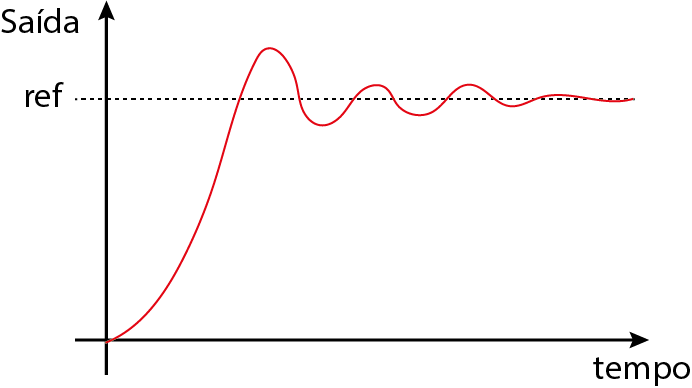
Tempo de súbida $(t_r)$
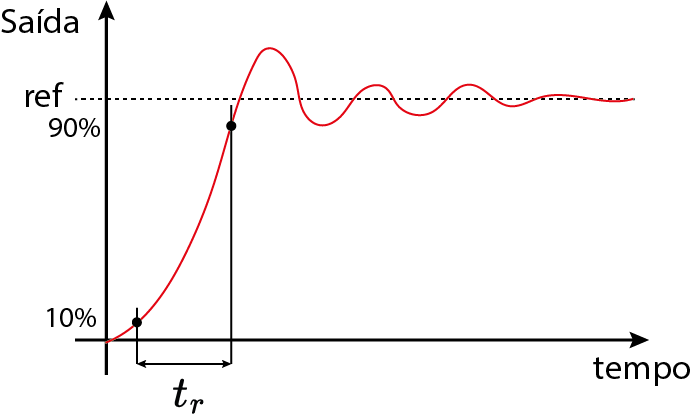
Sobresinal $(M_p)$
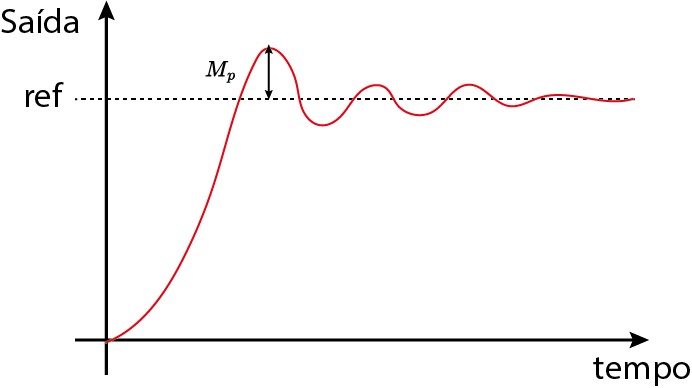
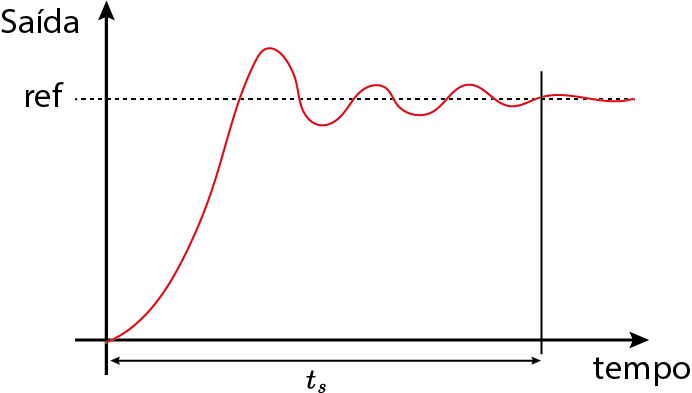
Tempo de acomodação $(t_s)$
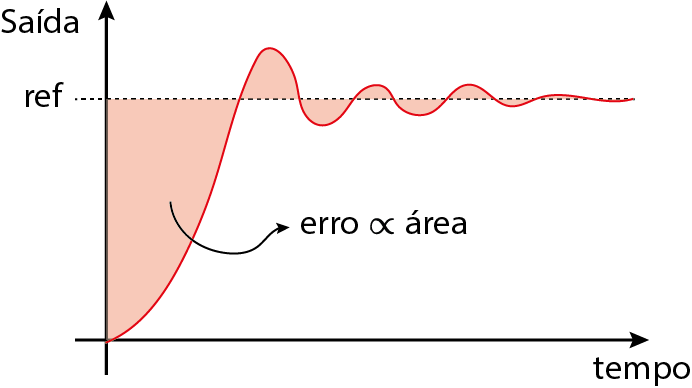
Erro $(\epsilon)$
Controlador
O controlador resultante do projeto é um objeto matemático.
- Abordagem em frequência: $$C(s)=\frac{N(s)}{D(s)}$$
- Abordagem no domínio do tempo: $$u(t)=C\{x(t)\}$$
Implementação
Analógico vs Digital
 |  |
| Resistores, capacitores, indutores e OpAmp. | Computador digital ($\mu C$) |
Pólos
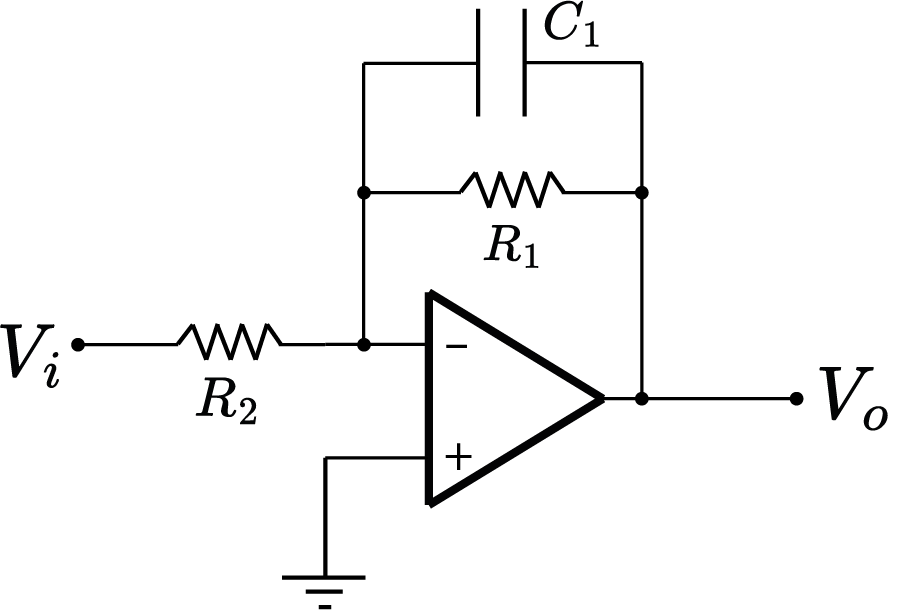 $$
\frac{V_o}{V_i}=-\frac{R_1}{R_2}\frac{\frac{1}{R_1C_1}}{s+\frac{1}{R_1C_1}}
$$
$$
\frac{V_o}{V_i}=-\frac{R_1}{R_2}\frac{\frac{1}{R_1C_1}}{s+\frac{1}{R_1C_1}}
$$
Zeros
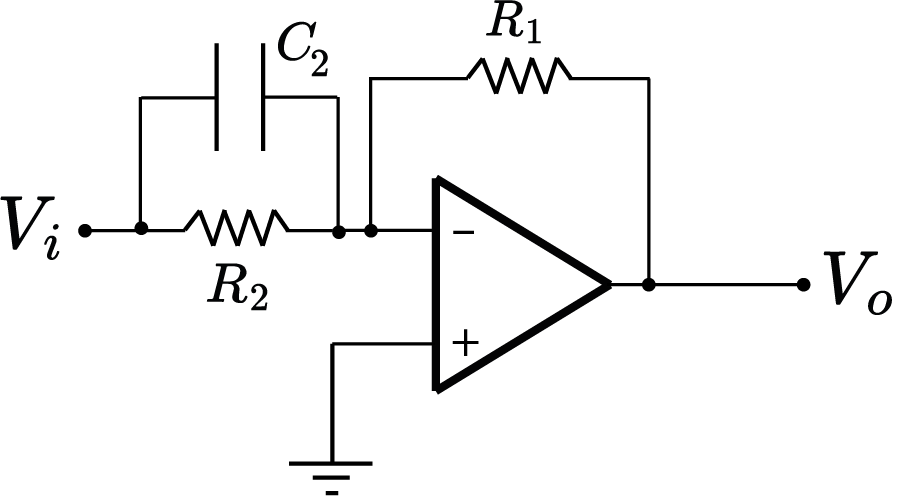 $$
\frac{V_o}{V_i}=-R_1C_2(s+\frac{1}{R_2C_2})
$$
$$
\frac{V_o}{V_i}=-R_1C_2(s+\frac{1}{R_2C_2})
$$
Implementação
Analógico vs Digital
 |  |
| Resistores, capacitores, indutores e OpAmp. | Computador digital ($\mu C$) |
Controle Digital

Computador digital ($\mu C$)
Controle Digital
Vantagens:
 |
|
Controle Digital

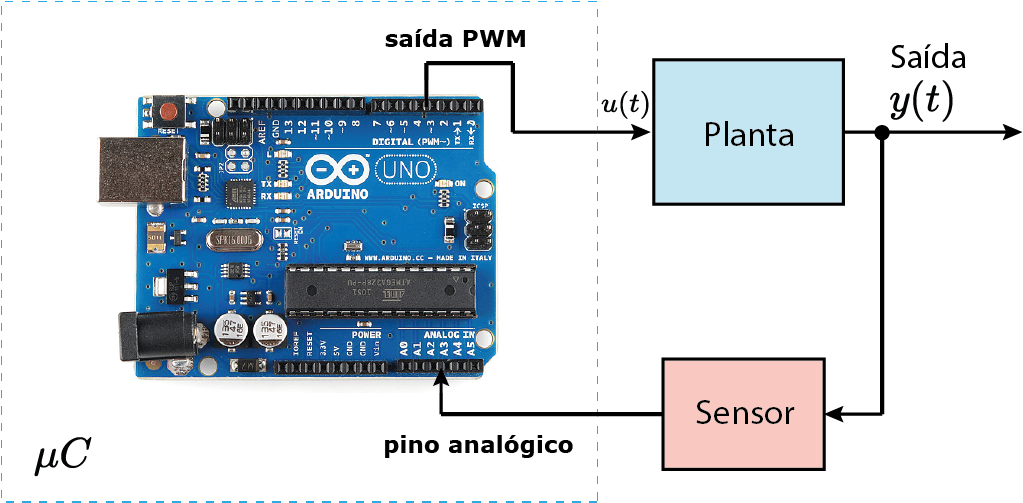
Interface analógica/digital
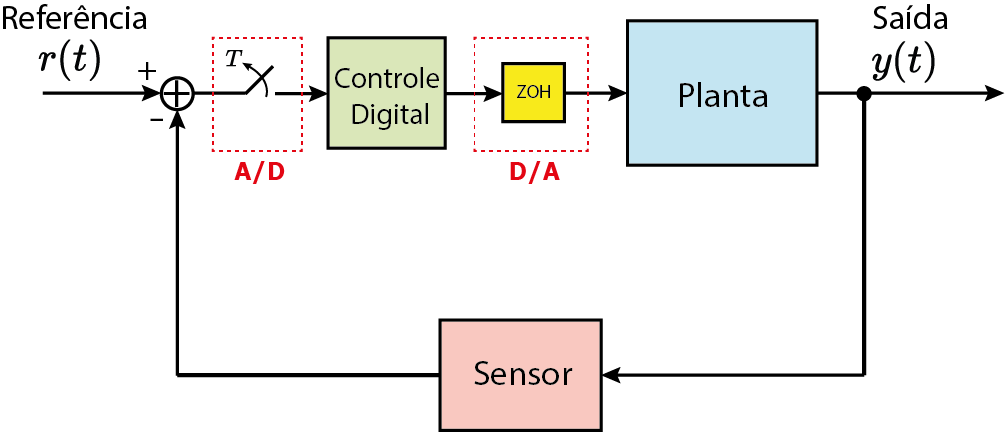
Interface analógica/digital
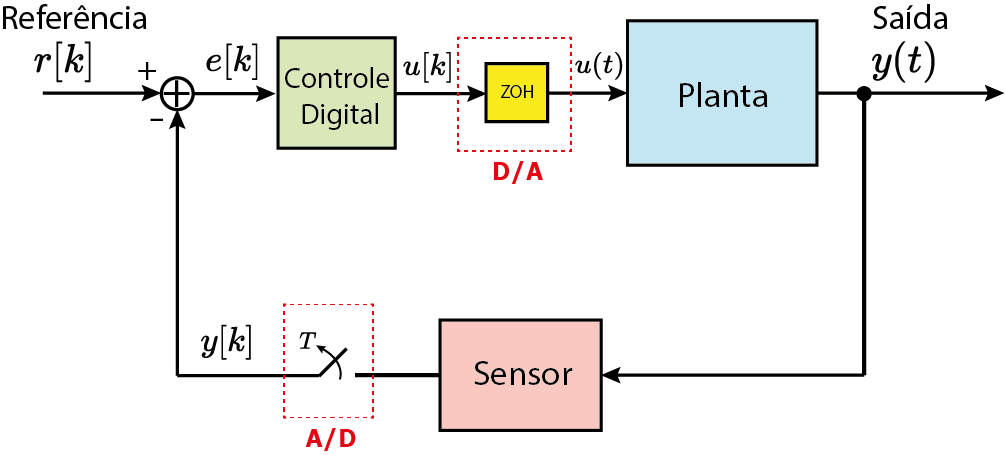
Interface analógica/digital
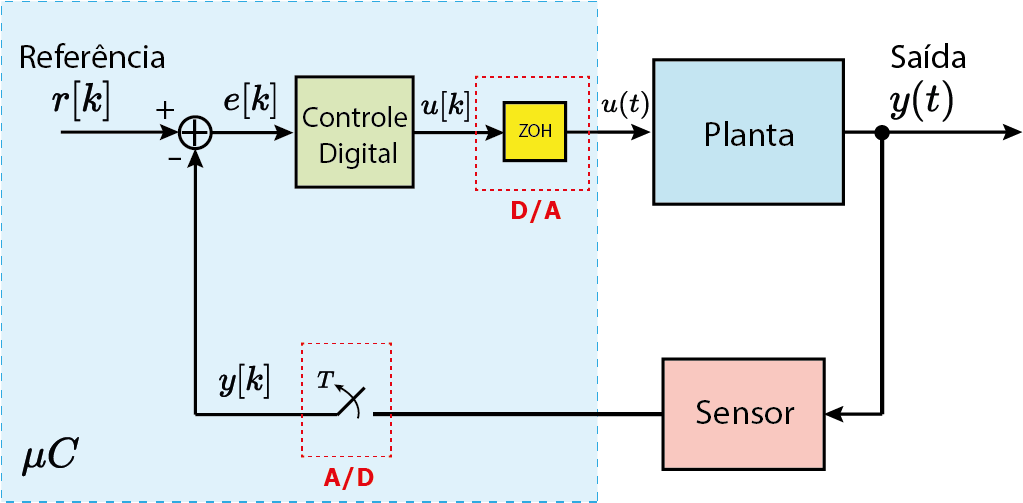
Interface analógica/digital
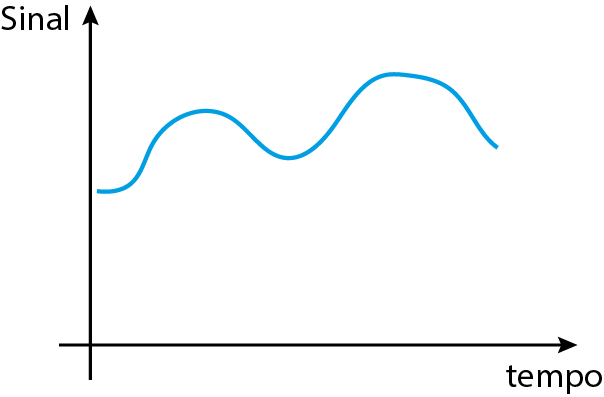
Sinal digital
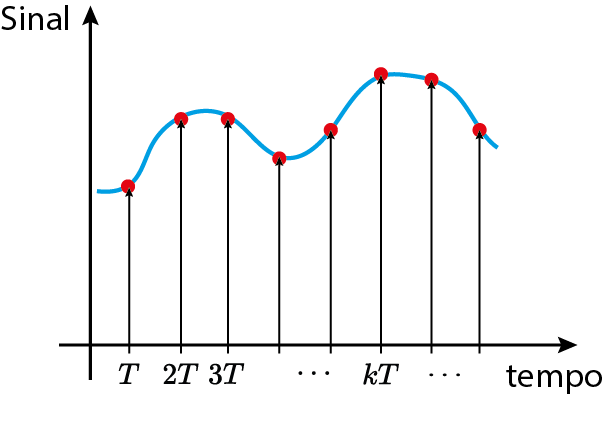
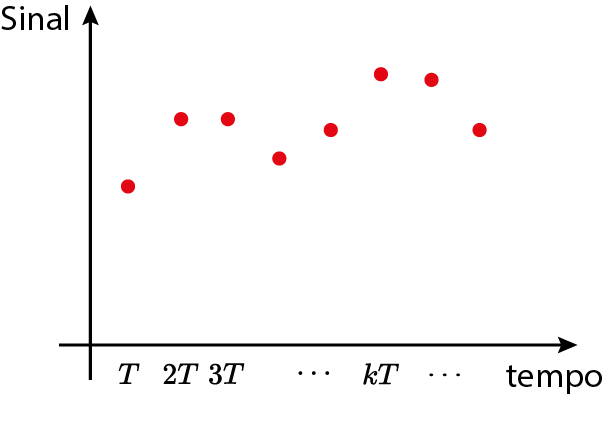
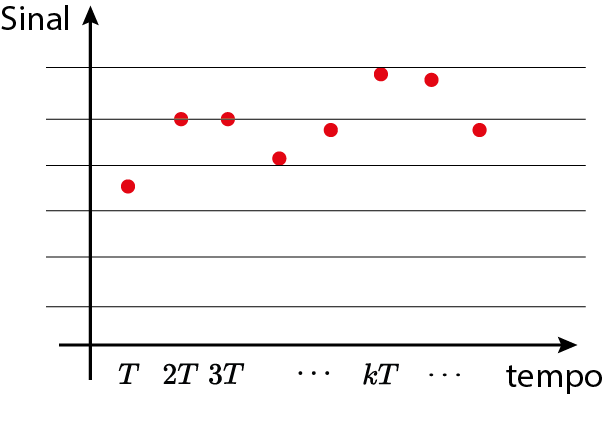
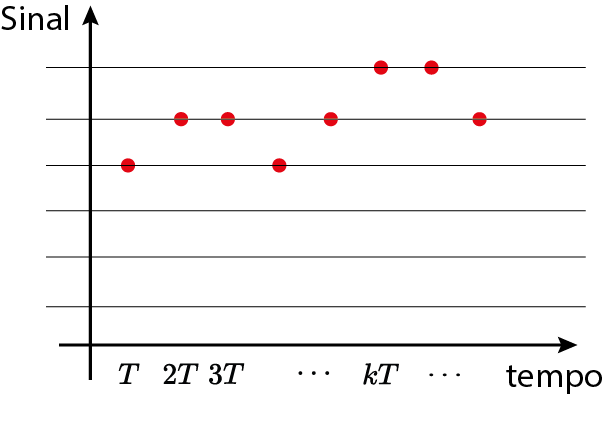
Escolha do tempo de amostragem

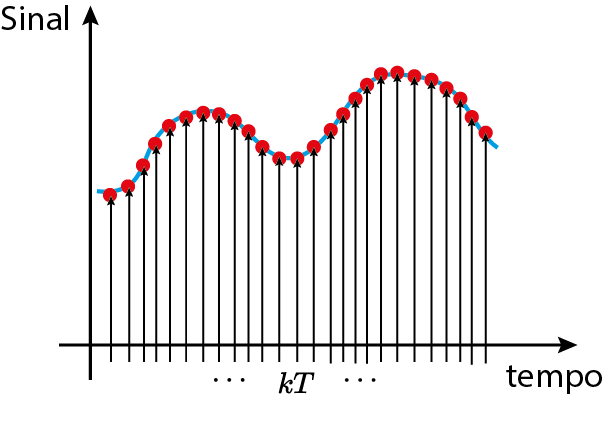
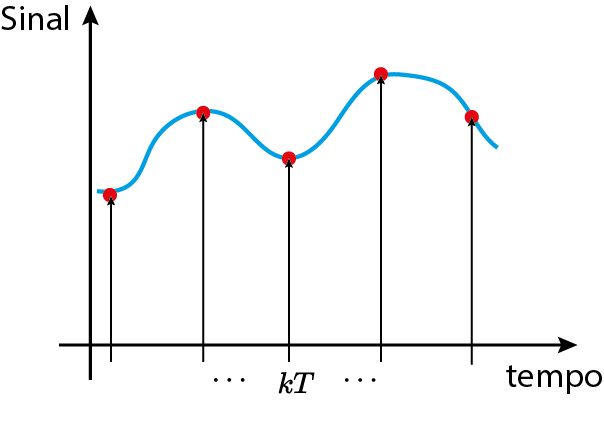
Sequência de números

Transformada Z
$$X(z)=\sum_{k=-\infty}^\infty x[k]z^{-k}$$Representação de sistemas
Funções de transferência (domínio $z$):
$$\frac{Y(z)}{U(z)}=G(z)$$ em que $$ z=e^{sT}$$
Equações à diferenças:
$$\sum_{n=0}^N a_ny[k-n]=\sum_{m=1}^M b_m u[k-m]$$Sequência de Fibonacci
$$y_k=y[k-1]+y[k-2]$$ com $$ \begin{cases} y[0]=0\\ y[1]=1 \end{cases} $$

Análise de estabilidade
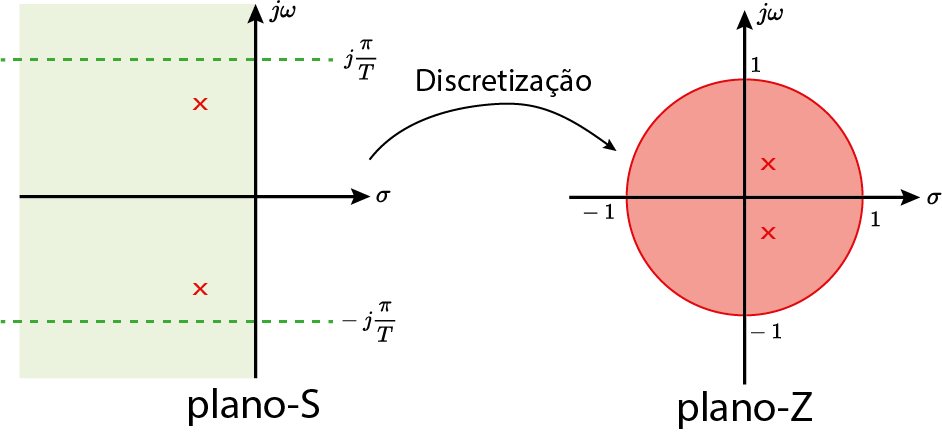
Testes
- Simulações computacionais;



Testes
- Direto na planta (de forma segura);

Exemplos de controladores

On-off
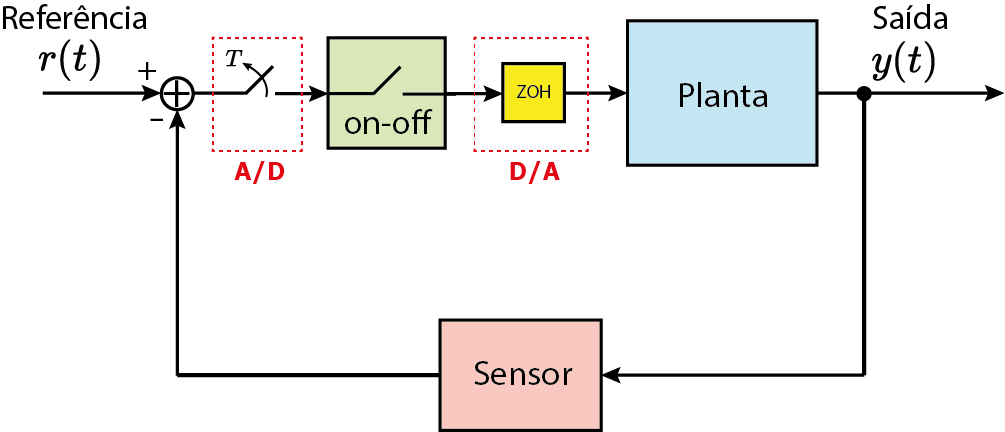
Utilizado em geladeiras, ar-condicionados, caixas de água etc
On-off
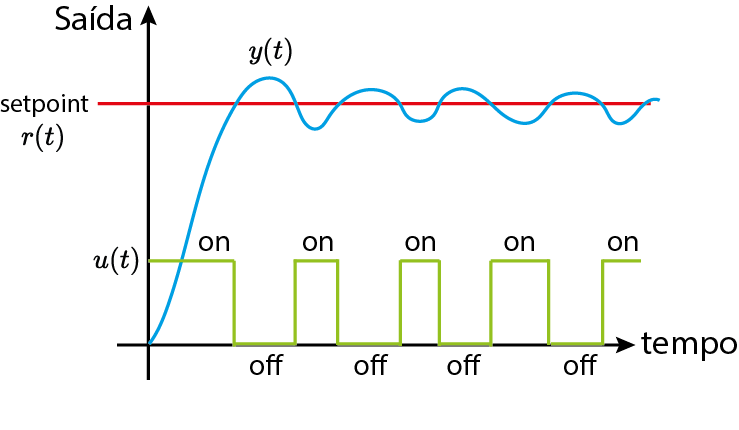
PID
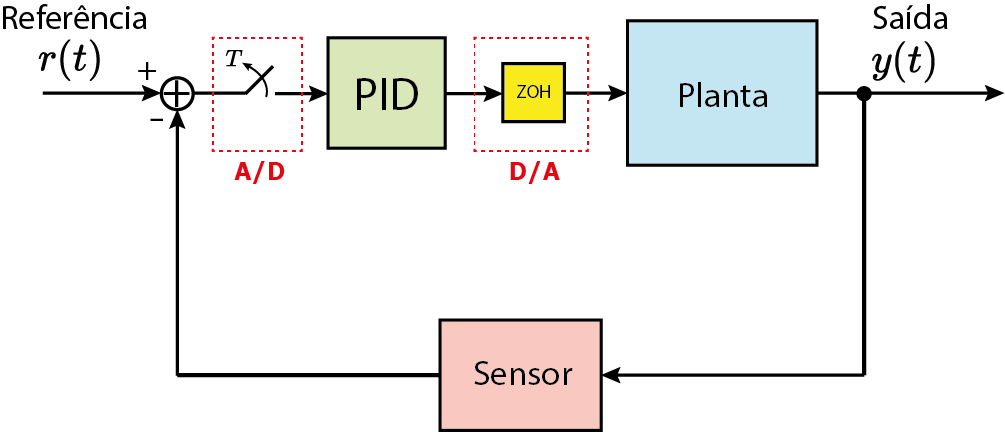
PID (tempo contínuo)
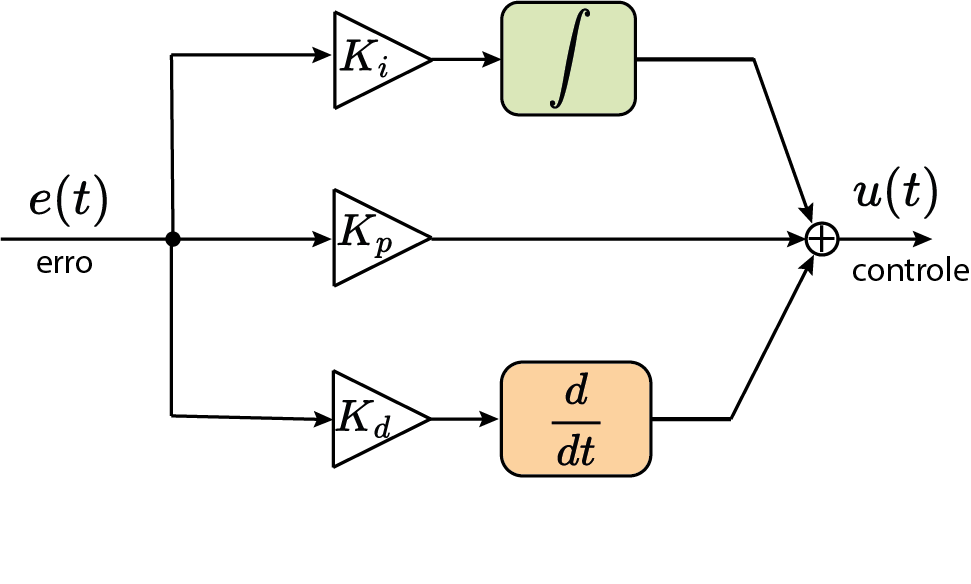
$C(s)=K_p+K_i\frac{1}{s}+K_ds$
PID (tempo discreto)
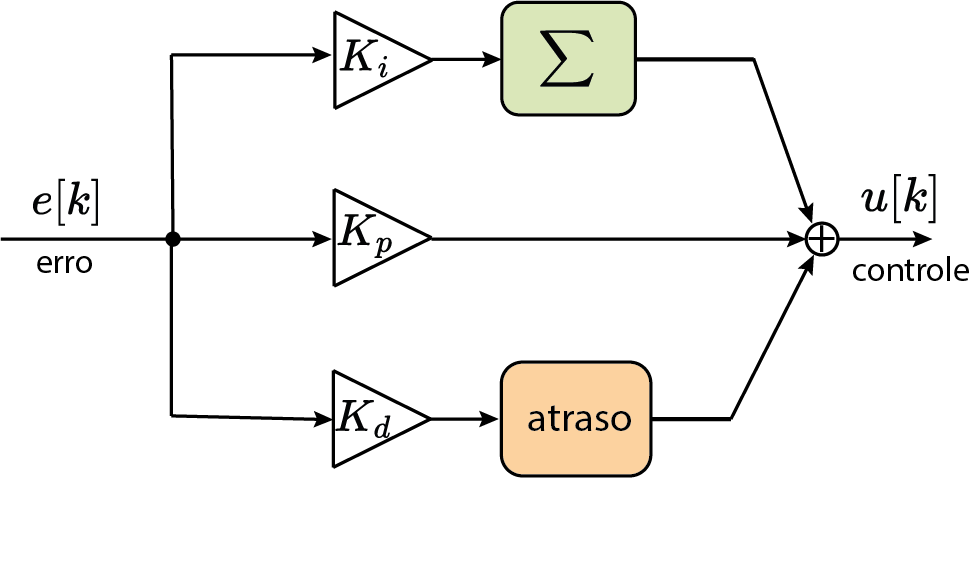
$C(z)=K_p+K_i\frac{1}{1-z^{-1}}+K_d(1-z^{-1})$
Exemplos de controladores
LQR (Linear Quadratic Regulator)
Dado um sistema modelado em espaço de estados:
$$x_{k+1}=Ax_k+Bu_k$$ Busca-se a lei de controle que minimiza o custo $$J=\sum_{k=0}^T x_k^TQx_k+u_k^TRu_k$$Exemplos de controladores
Realimentação de estados
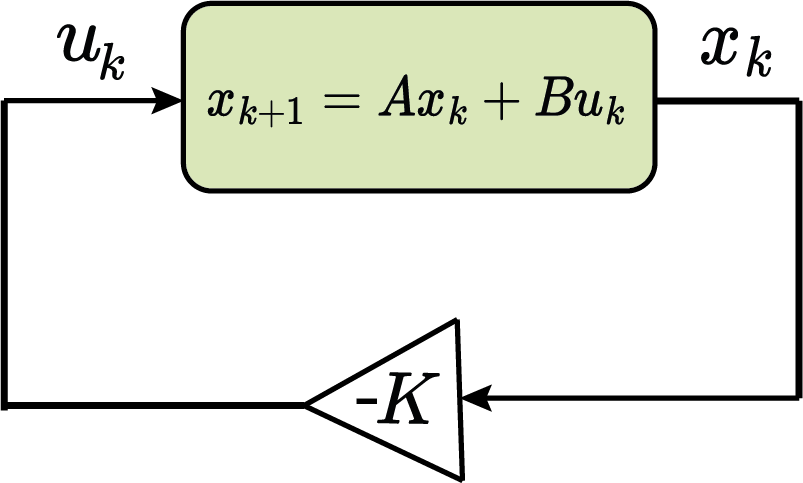
Controle ótimo: LQR
Observador de estados
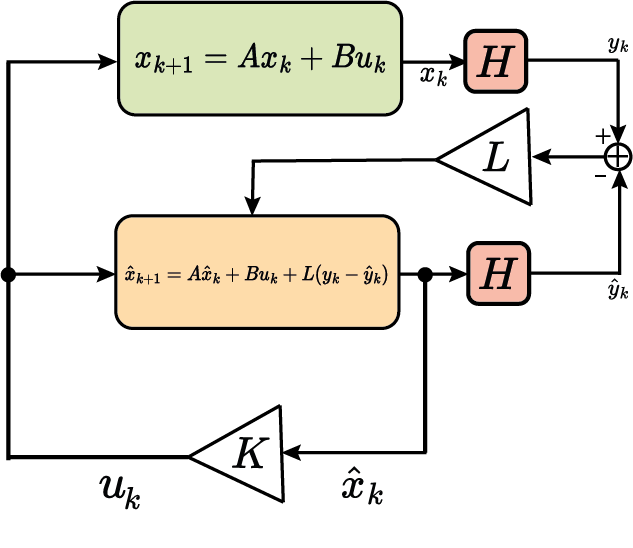
Observador ótimo: Filtro de Kalman
Próxima aula teórica
Teorema da amostragem
