

Aula 1:
Introdução à disciplina Sinais e Sistemas
SEL0604
Prof. Marcos Rogério Fernandes
5 de agosto de 2024
Objetivos
Os objetivos dessa aula são:
- Apresentar a disciplina: estrutura e avaliação;
- Introduzir conceitos básicos de sinais e sistemas;
- Ilustrar as aplicações de sinais e sistemas com exemplos práticos;
- Evidenciar a importância do estudo de sinais e sistemas para engenharia.
- *Começar revisão de álgebra linear.
SEL0604 - Sinais e Sistemas
Dúvidas:
Contato: marofe@usp.br
SEL0604 - Sinais e Sistemas
Monitoria:
- a definir...
Tópicos
- Propriedades de sinais;
- Representação de sinais no tempo;
- Representação de sinais na frequência;
- Series de Fourier e suas aplicações;
- Transformada de Fourier e suas aplicações;
- Filtragem de sinais;
- Representação e Propriedades de sistemas;
- Sistemas Lineares Invariantes no Tempo (SLIT);
- Transformada de Laplace e suas aplicações.
Material da disciplina

- Slides;
- Notas de aula;
- Listas de exercícios;
- Vídeos relacionados aos tópicos;
- Códigos, exemplos ilustrativos, etc...
Material da disciplina
Referências
- [1] E.R. Martins. Essentials of Signals and Systems. Wiley, 2023.
- [2] J.C. Geromel and G.S. Deaecto. Análise linear de sinais: teoria, ensaios práticos e exercícios. Editora Blucher, 2019.
- [3] J.C. Geromel and A.G.B. Palhares. Análise linear de sistemas dinâmicos. Editora Blucher, 2019.
- [4] Alan V. Oppenheim, Alan S. Willsky, and S. Hamid Nawab. Signals & systems (2nd ed.). Prentice-Hall, Inc., USA, 1996.
Avaliação
Serão realizadas:
- Três provas: $P_1$, $P_2$ e $P_3$;
- Listas de exercícios: $L_1,L_2,L_3,\cdots,L_n$;
- Ao final do semestre, um trabalho computacional $T$.
Avaliação
$\Rightarrow $Cada aula terá um conjunto de exercícios propostos;
$\Rightarrow $As provas serão baseadas nos exercícios propostos nas aulas;
$\Rightarrow $As listas $L_1, L_2, L_3,\cdots,L_n$ serão compostas por 5 dos exercícios propostos nas aulas (escolha livre);
$\Rightarrow$ As listas poderam se entregues em até 2 semanas após a respectiva aula no e-disciplina;
Avaliação
A média final é dada por:$$MF=0.6P+0.3L+0.1T$$
$$P=mean(P_1,P_2,P_3)$$ $$L=mean(L_1,L_2,L_3,\cdots,L_n)$$
Avaliação
Para aprovação, é necessário:
- Ao menos $70\%$ de frequência, $MF\ge 5.0$.
- Se $3.0\le MF < 5.0$, aluno ficará de recuperação.
- Se $MF<3.0$ ou menos de $70\%$ de frequência o aluno é reprovado.
Dúvidas?

Introdução
O que é um sinal?
Sinal é tudo que carrega informação.
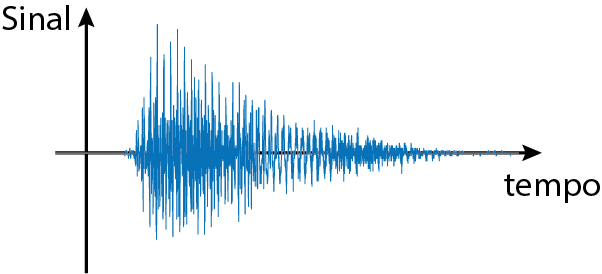
O que é um sistema?
Sistema é tudo que modifica um sinal.
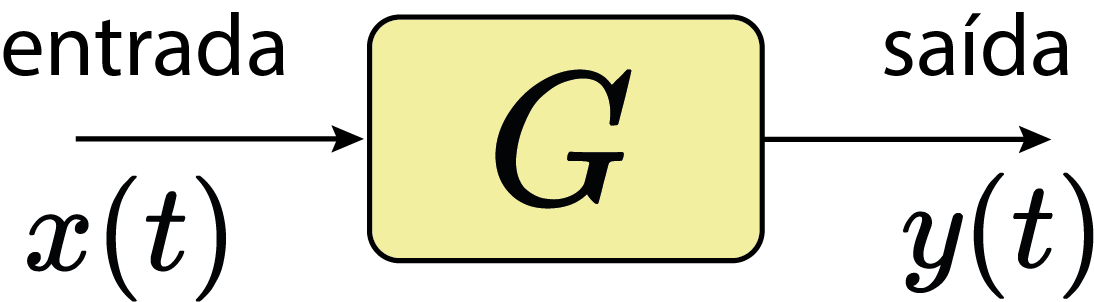
Sistema é tudo que modifica um sinal.
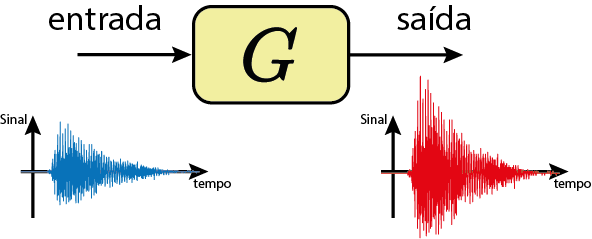
Exemplos de sinais e sistemas
Telecomunicações


Telecomunicações

Internet
Indústria: variáveis de processo

Carros inteligentes

Corpo Humano
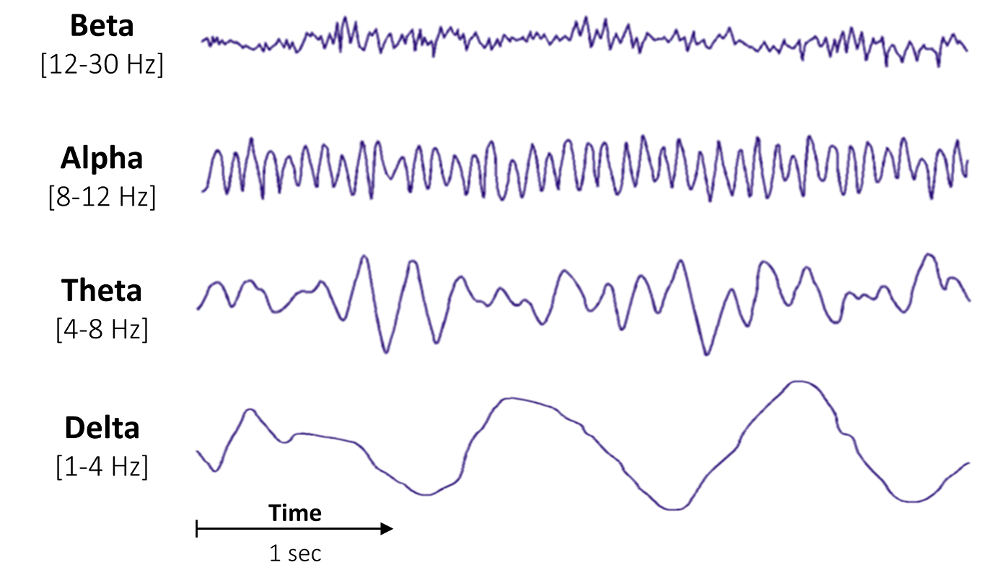
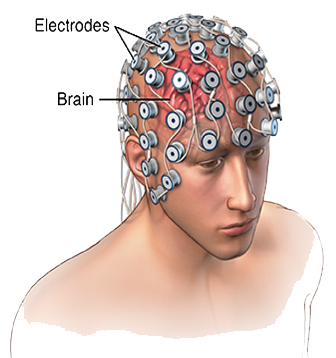
Corpo Humano
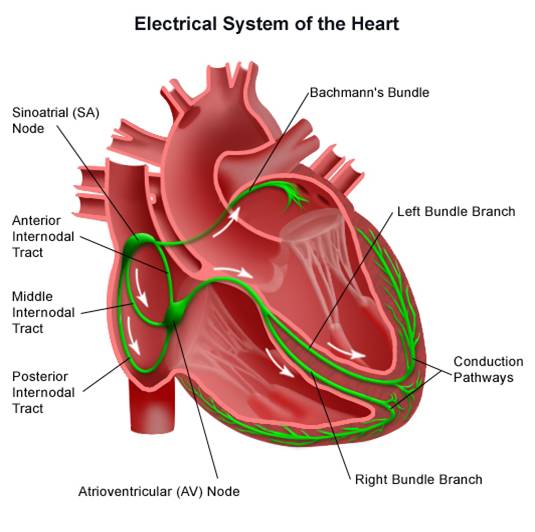
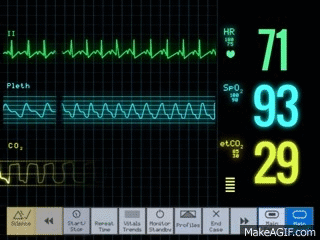
Mercado Financeiro
Objetivo principal do curso
Aprender propriedades que os sinais obdecem quando passam por uma classe especial de sistemas:
Sistemas Lineares e Invariantes no Tempo (SLIT)
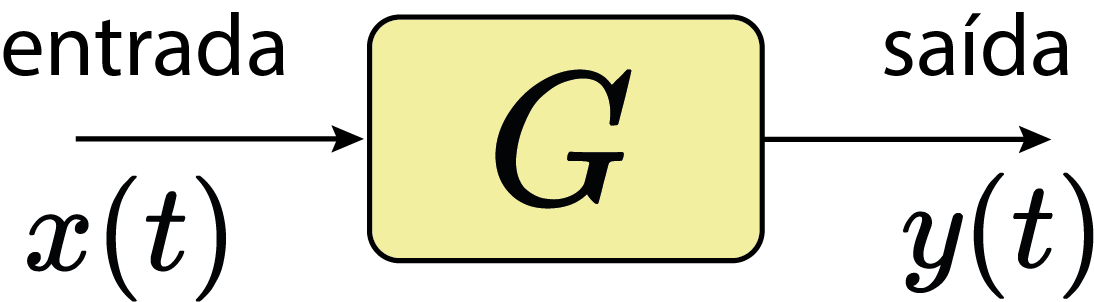
Representação matemática
Função matemática $g:\mathbb{R}\to\mathbb{R}$

Os mesmos conceitos são validos para dimensões maiores
($\mathbb{R}^2,\mathbb{R}^3$,...$\mathbb{R}^n$)
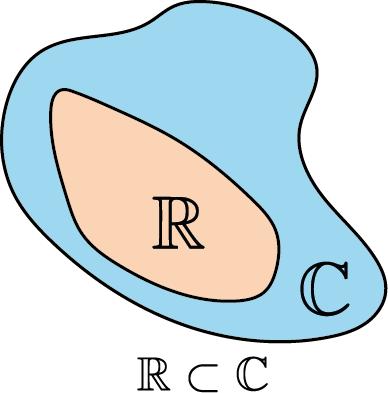
Função matemática $g:\mathbb{R}\to\mathbb{C}$
Números complexos trazem benefícios na análise de sinais.
Número Complexo
$$z=a+jb$$
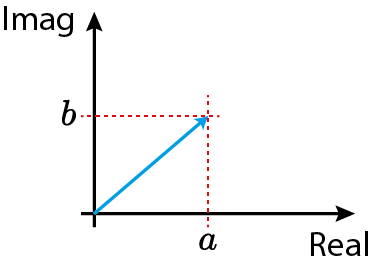
$j=\sqrt{-1}$
Exponencial Complexa
$$z=re^{j\omega t}$$
Fórmula de Euler
$$\Large e^{j\omega t}=\cos(\omega t)+j\sin(\omega t)$$
Classificações dos sinais
Tempo Contínuo vs Tempo Discreto
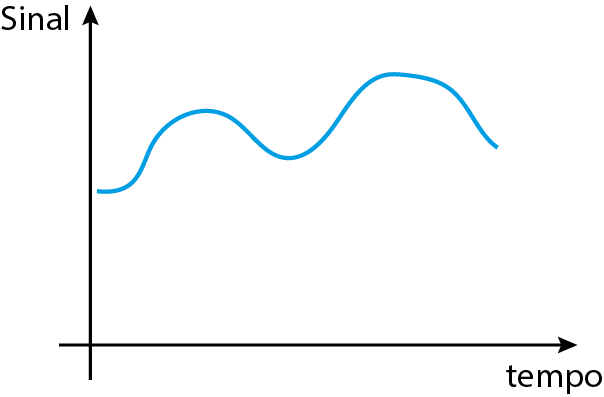
$g:\mathbb{R}\to\mathbb{R}$
Tempo Contínuo vs Tempo Discreto

$g:\mathbb{Z}\to\mathbb{R}$
Determinístico vs Estocástico

Ex: Tensão e corrente de um circuito elétrico.
Determinístico vs Estocástico
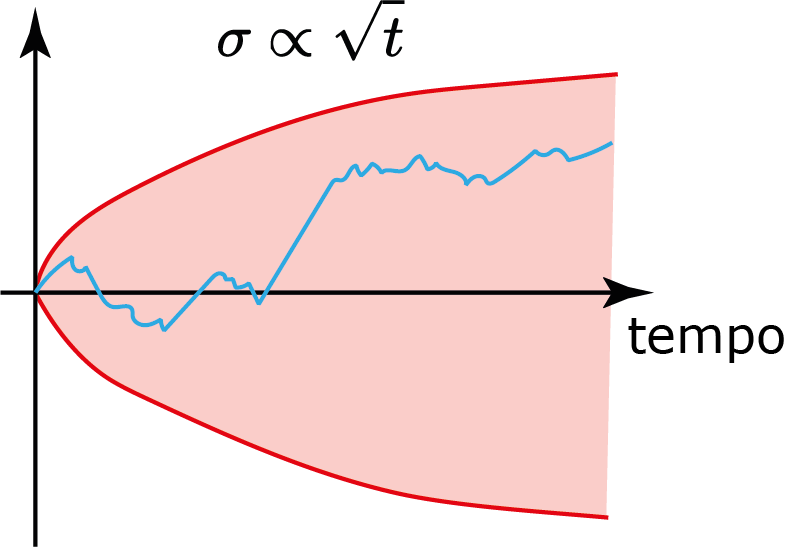
Ex: mercado de ações, volume de chuvas, etc.
Propriedades dos sinais
Sinal de energia
$$\begin{equation} E=\int_{-\infty}^\infty g(t)^2dt < \infty \end{equation}$$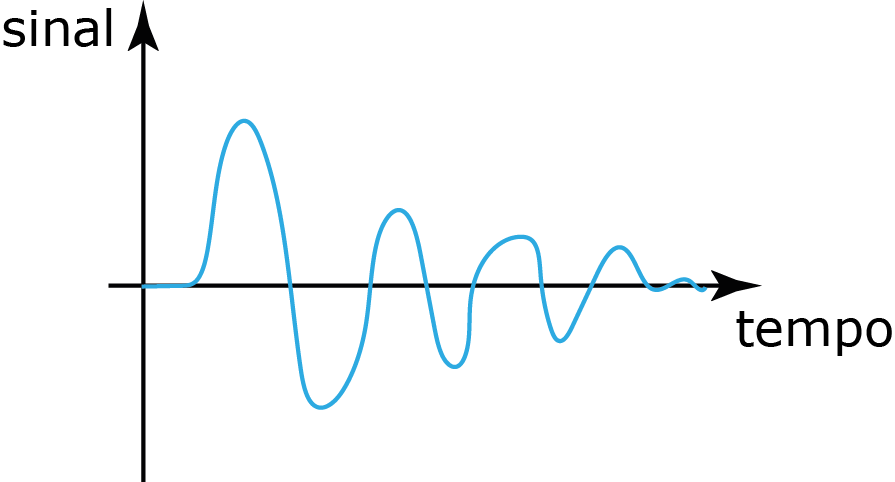
Sinal de energia
$$\begin{equation} E=\int_{-\infty}^\infty g(t)^2dt < \infty \end{equation}$$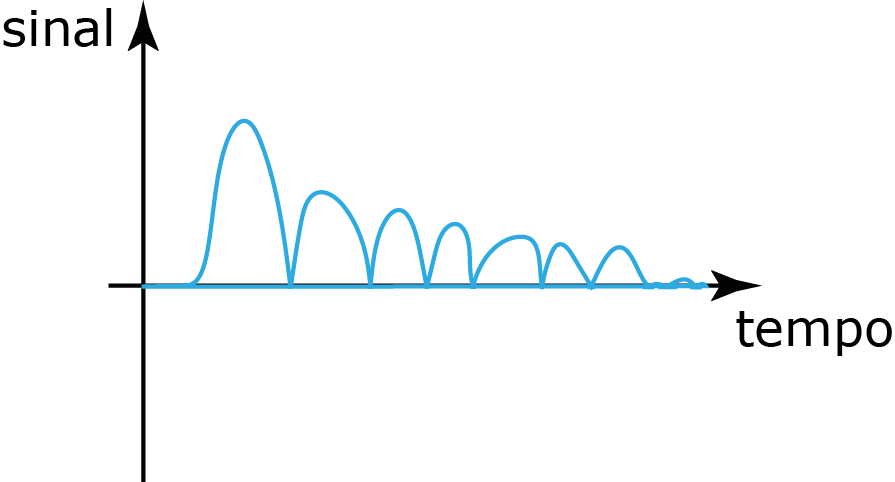
Sinal de energia
$$\begin{equation} E=\int_{-\infty}^\infty g(t)^2dt < \infty \end{equation}$$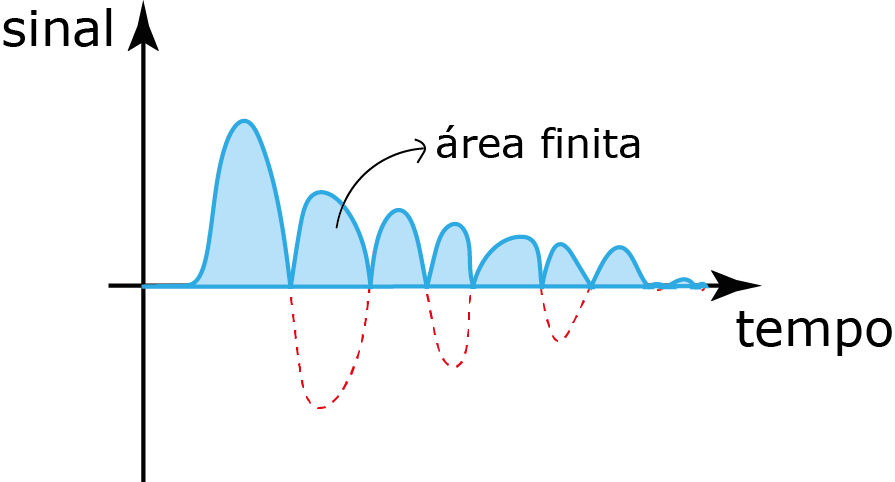
Sinal de energia
$$\begin{equation} E=\int_{-\infty}^\infty g(t)^2dt < \infty \end{equation}$$
Sinais de energia são utilizados para transmitir informação!
Sinal de potência
$$\begin{equation} P_\text{med}= \lim_{\tau\to\infty} \frac{1}{2\tau}\int_{-\tau}^\tau g(t)^2dt \end{equation}$$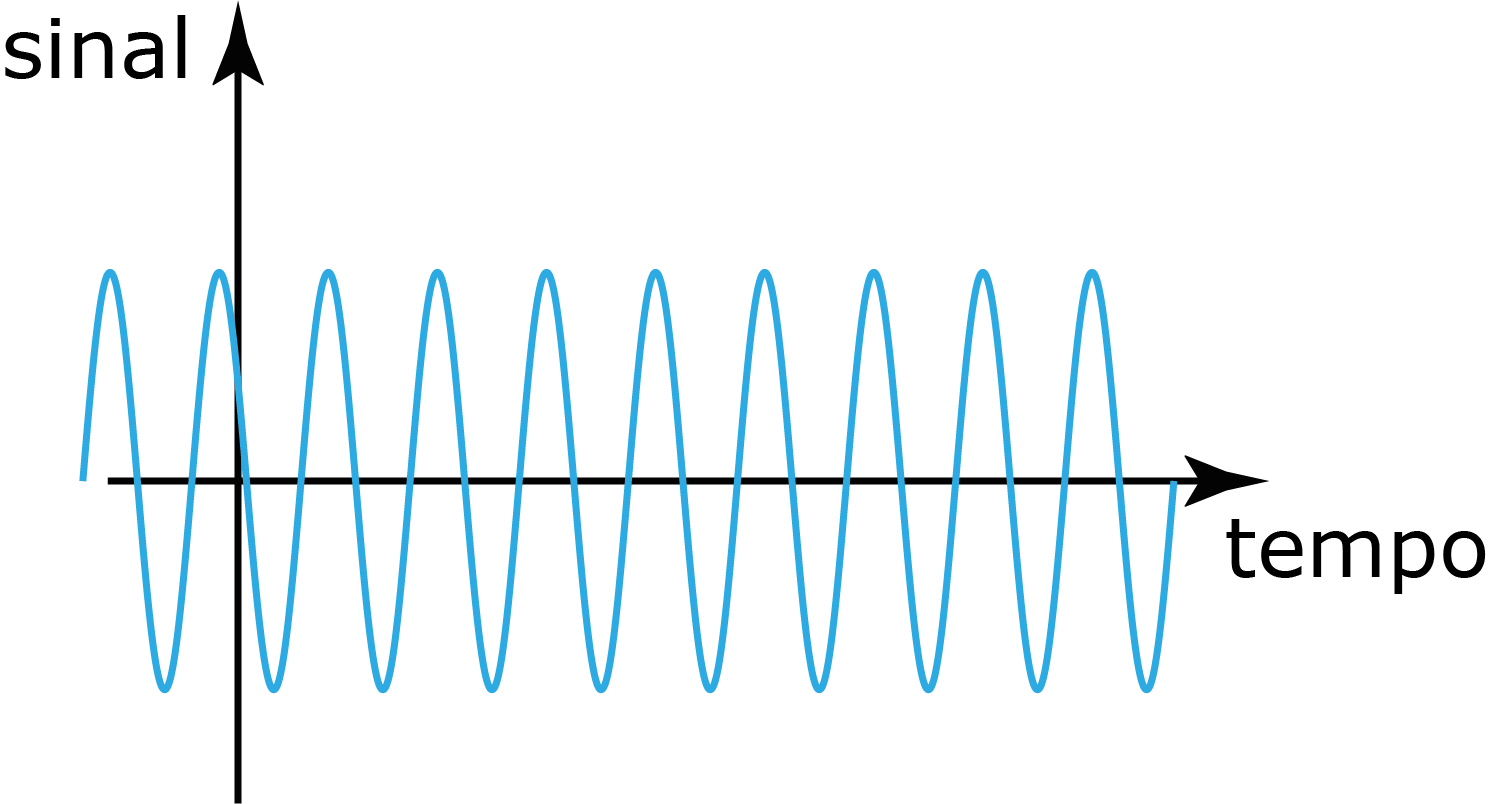
Sinal de potência
$$\begin{equation} P_\text{med}= \lim_{\tau\to\infty} \frac{1}{2\tau}\int_{-\tau}^\tau g(t)^2dt \end{equation}$$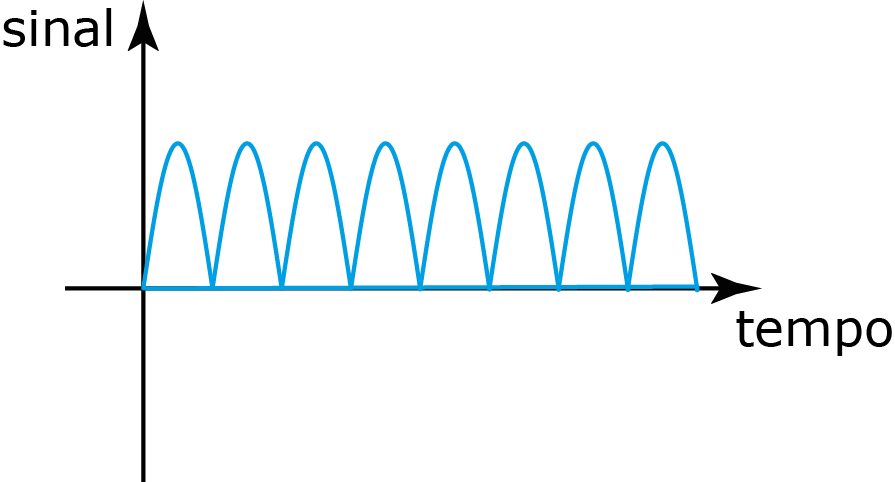
Sinal de potência
$$\begin{equation} P_\text{med}= \lim_{\tau\to\infty} \frac{1}{2\tau}\int_{-\tau}^\tau g(t)^2dt \end{equation}$$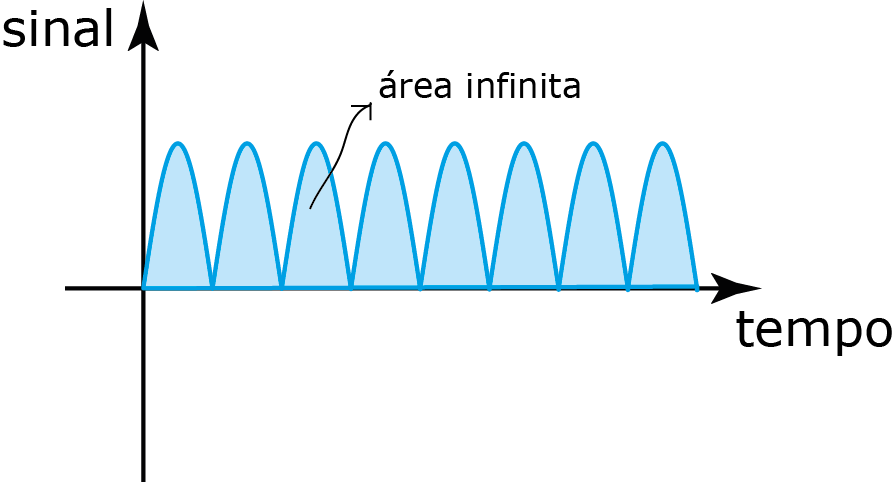
Sinal de potência
$$\begin{equation} P_\text{med}= \lim_{\tau\to\infty} \frac{1}{2\tau}\int_{-\tau}^\tau g(t)^2dt \end{equation}$$
Sinais de potência são utilizados para fornecer energia para um sistema!
Energia vs Potência
$$\begin{equation} E=\int_{-\infty}^\infty g(t)^2dt \end{equation}$$ $$\begin{equation} P_\text{med}= \lim_{\tau\to\infty} \frac{1}{2\tau}\int_{-\tau}^\tau g(t)^2dt \end{equation}$$Sinal de energia não pode ser sinal de potência e vice-versa
Sinal ímpar:
$$ g(t)=-g(-t),\quad \forall t\in\R $$Sinal ímpar:
$$ g(t)=-g(-t),\quad \forall t\in\R $$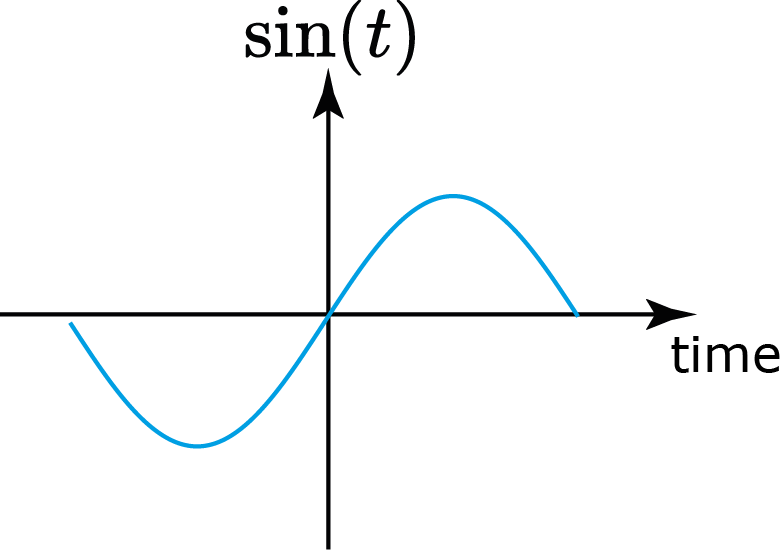
Sinal ímpar:
$$ g(t)=-g(-t),\quad \forall t\in\R $$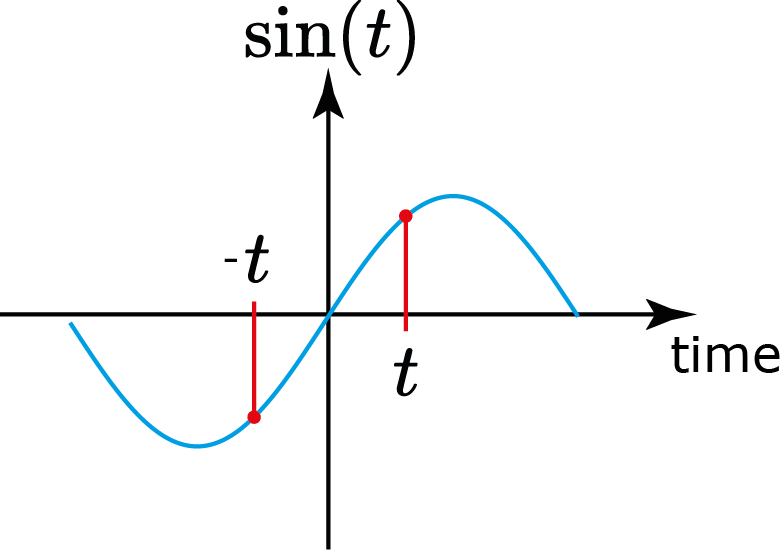
Sinal par:
$$ g(t)=g(-t),\quad \forall t\in\R $$Sinal par:
$$ g(t)=g(-t),\quad \forall t\in\R $$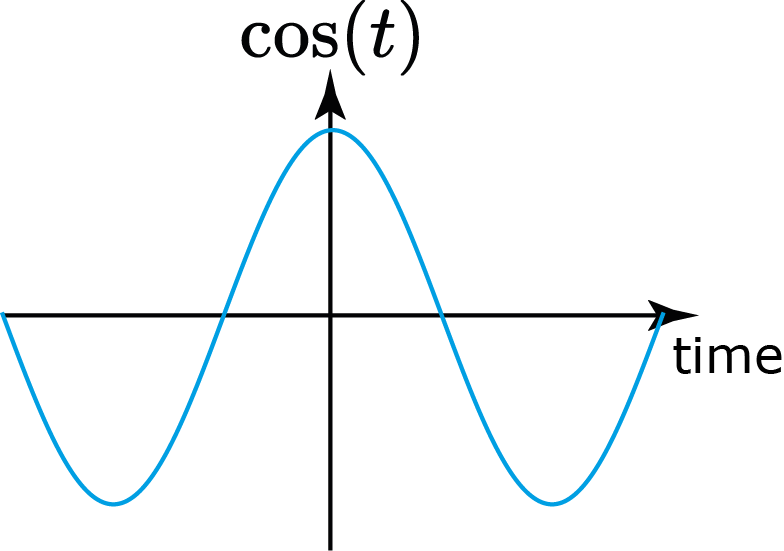
Sinal par:
$$ g(t)=g(-t),\quad \forall t\in\R $$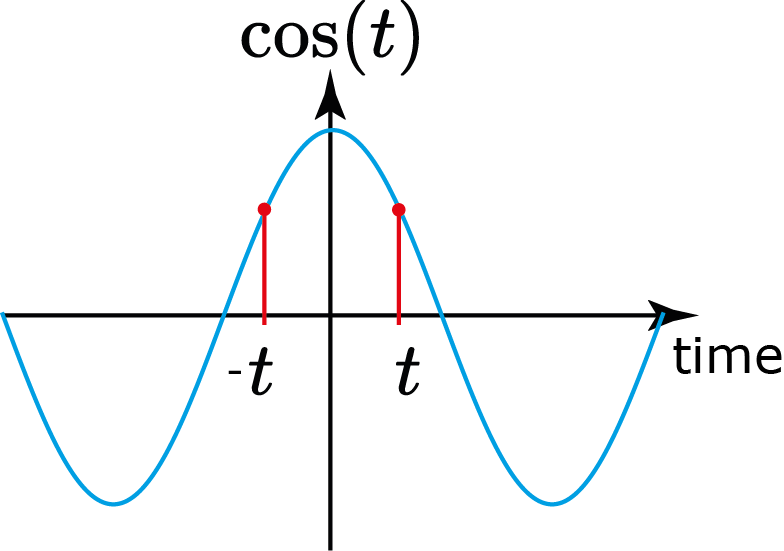
Todo sinal pode ser escrito como a soma da parte par com a ímpar
$$g(t)=g_p(t)+g_i(t)$$ em que $$\small\begin{align*} g_p(t)&=\frac{1}{2}(g(t)+g(-t))\\ g_i(t)&=\frac{1}{2}(g(t)-g(-t)) \end{align*}$$Sinais especiais
- Degrau Unitário;
- Retângulo Unitário;
- Sinc (seno normalizado);
- Impulso Unitário;
Degrau unitário

Retângulo unitário (Gate)
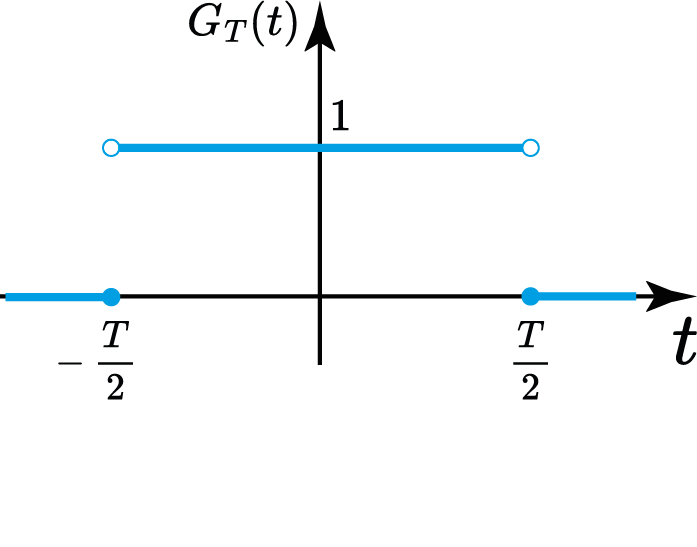
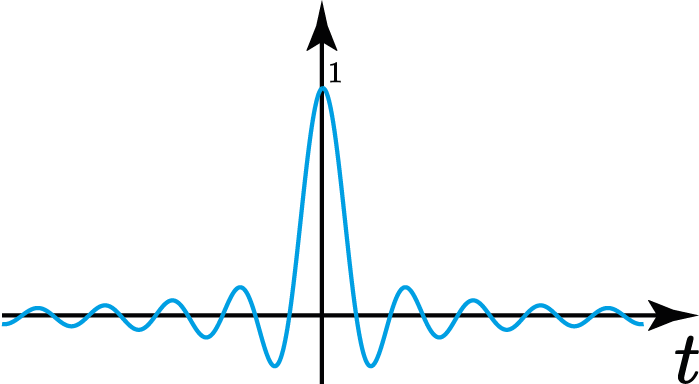
Sinc (seno normalizado)
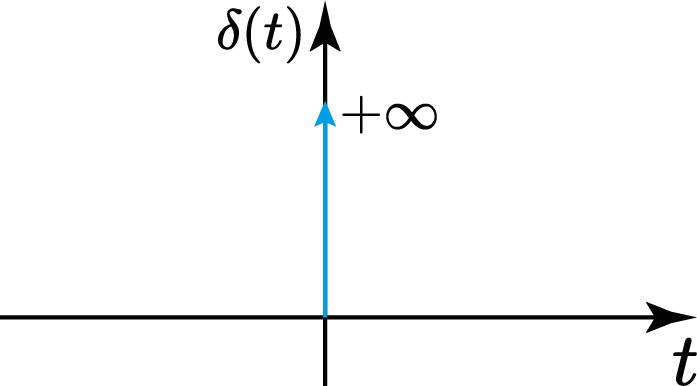
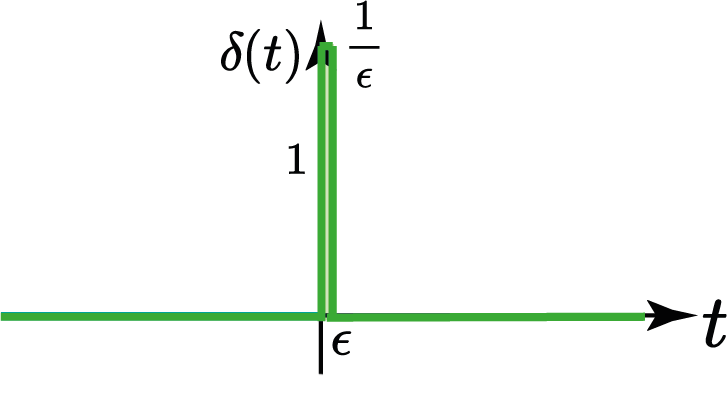
Impulso unitário (Delta de Dirac)
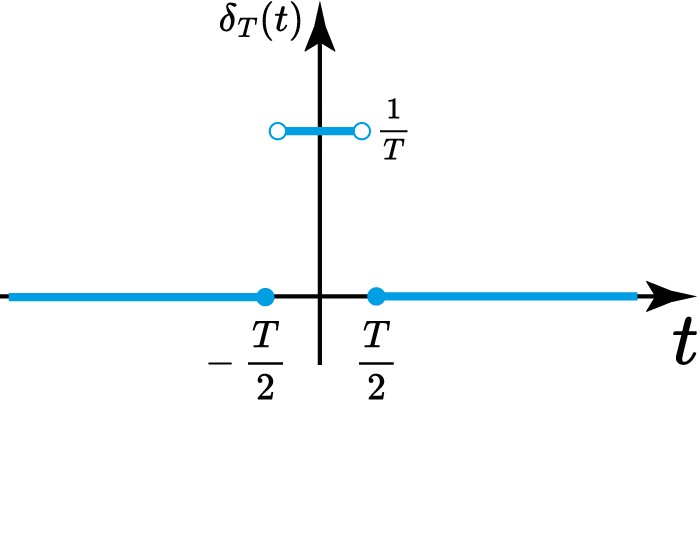
Impulso unitário (Aprox. Retângular)
Impulso unitário (Aprox. Retângular)
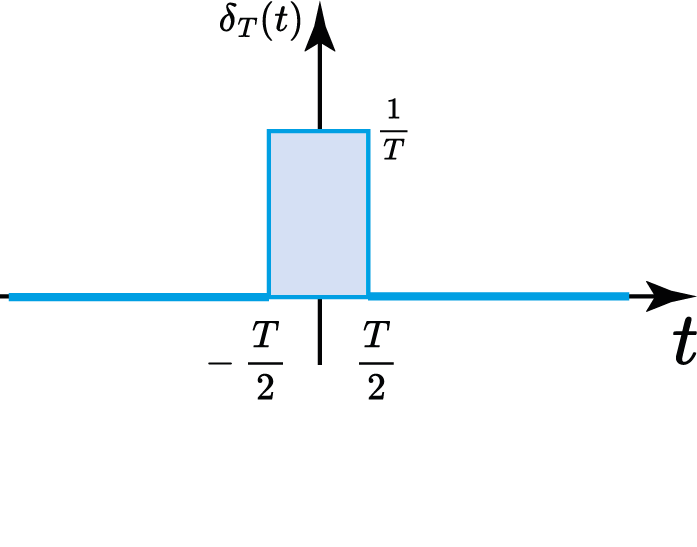
Impulso unitário (Aprox. Retângular)

Impulso unitário (Aprox. Retângular)
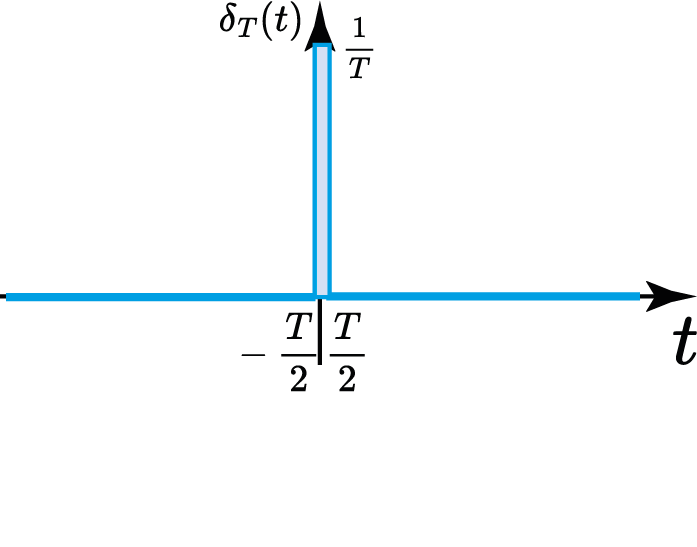
Impulso unitário "Derivada de $u(t)$"
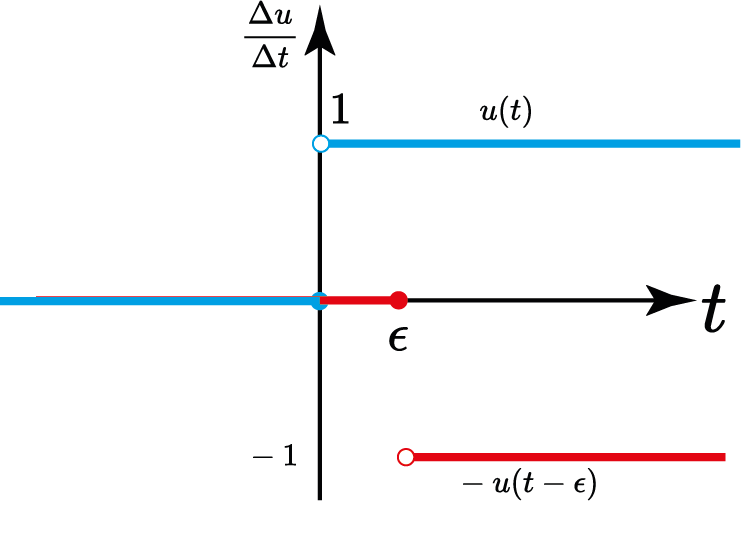
Impulso unitário "Derivada de $u(t)$"
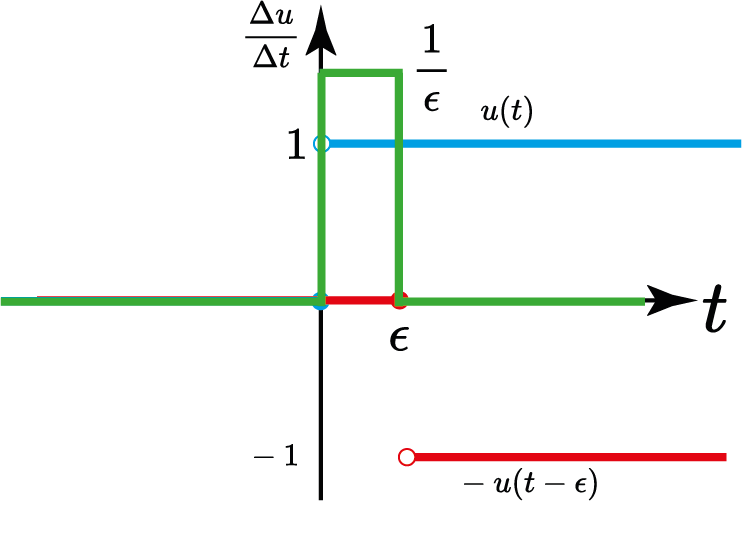
Impulso unitário "Derivada de $u(t)$"
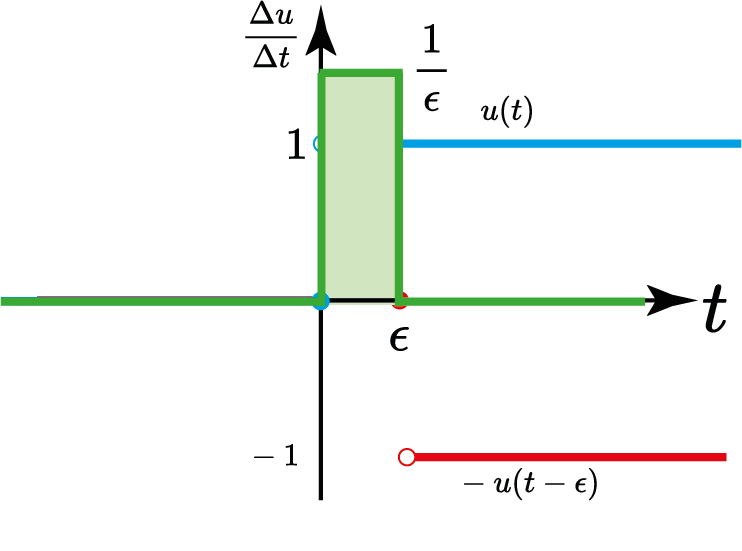
Impulso unitário "Derivada de $u(t)$"
PARTE II
Revisão de Álgebra
Revisão de Álgebra Linear
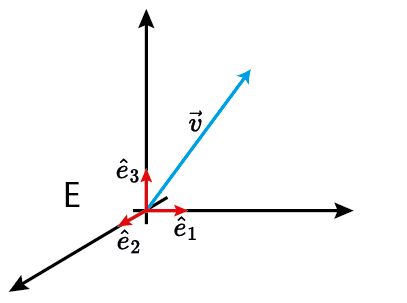
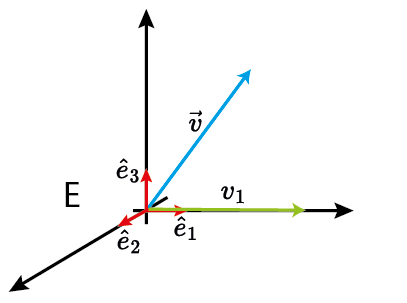
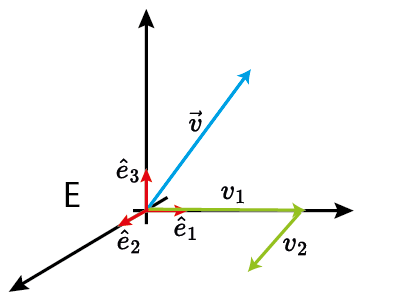
O que é um vetor?
$V$ é um espaço vetorial (ex: $\mathbb{R}^n$);
$E=\{\hat{e}_1,\ldots,\hat{e}_n\}$ é uma base de representação;
$\{v_1,\ldots,v_n\}$ são as coordenadas em relação a base $E$.
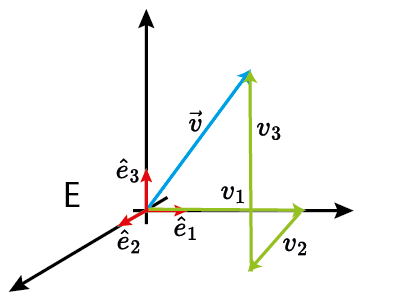

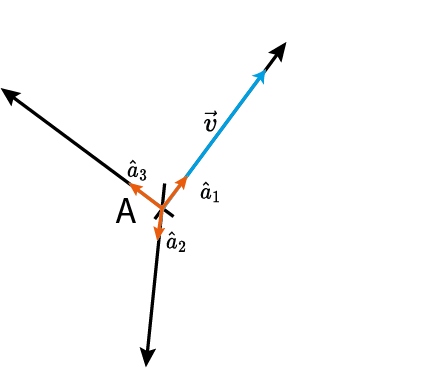
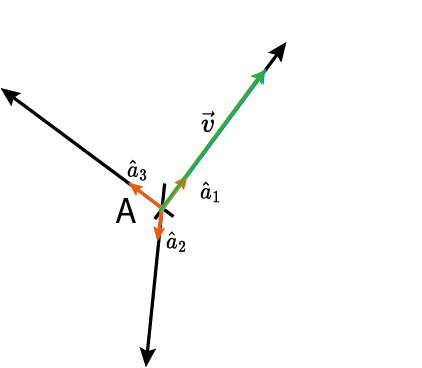
Revisão de Álgebra Linear
O que é um produto escalar?
- Resultado é um Escalar: $$\langle \vec v, \vec w\rangle = c, \text{ com } c \text{ é um escalar.}$$
- Linear pela direita: $$\langle \vec v, (\alpha \vec w_1 + \beta \vec w_2)\rangle = \alpha\langle \vec v,\vec w_1\rangle + \beta \langle \vec v,\vec w_2\rangle $$
Revisão de Álgebra Linear
O que é um produto escalar?
- Comutação: $$\langle \vec v, \vec w\rangle = \langle\vec w, \vec v\rangle ^*$$
Consequência $\Rightarrow $ combinação linear pela esquerda: $$\langle (\alpha\vec v_1 + \beta \vec v_2), w\rangle = \alpha^*\langle\vec v_1,\vec w\rangle + \beta^* \langle \vec v_2,\vec w\rangle $$
Revisão de Álgebra Linear
Combinação linear direita/esquerda
Revisão de Álgebra Linear
O que é uma norma?
Medida de distância dentro do espaço vetorial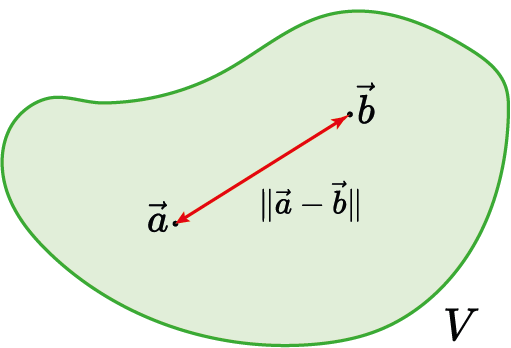
Medida de tamanho de um vetor
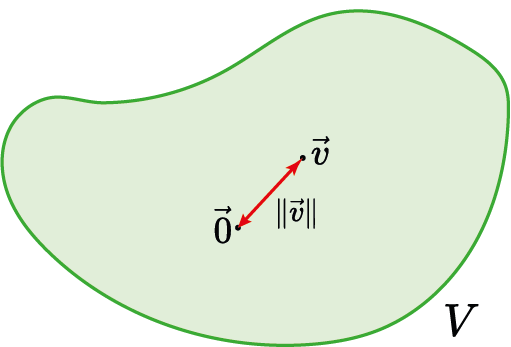
Se $\|\vec v\|=1$ então $\vec v$ é dito ser vetor unitário e é denotado por $\hat{v}$.

Revisão de Álgebra Linear
O que é uma projeção?


Revisão de Álgebra Linear
O que é ortogonalidade?
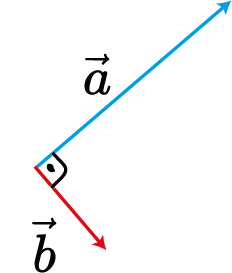

Revisão de Álgebra Linear
O que é uma base ortogonal?

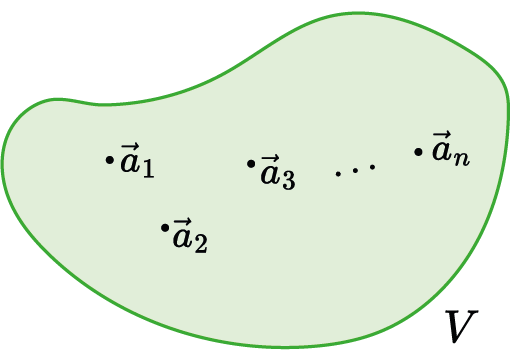
Revisão de Álgebra Linear
O que é uma base ortonormal?
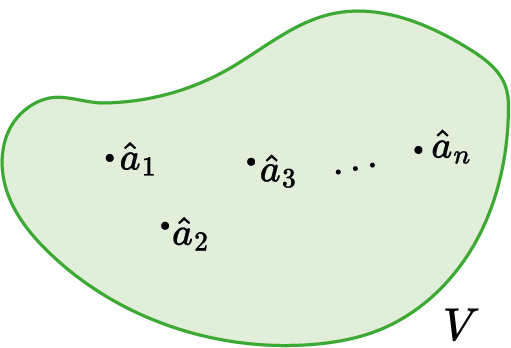
Revisão de Álgebra Linear
Representação de um vetor na base $A=\{\hat a_1,\cdots,\hat a_n\}$
Revisão de Álgebra Linear
Representação de um vetor na base $A=\{\hat a_1,\cdots,\hat a_n\}$
Próxima aula
Continuação da revisão de álgebra linear