

Aula 13:
Filtros Analógicos - parte 1
SEL0604
Prof. Marcos Rogério Fernandes
07 de outubro de 2024
Filtros Ideais
- Filtro Passa-Baixa (FPB);
- Filtro Passa-Alta (FPA)
- Filtros Passa-Faixa (FPF).
- Filtros Rejeita-Faixa (FRF).
Filtros Passa Baixa
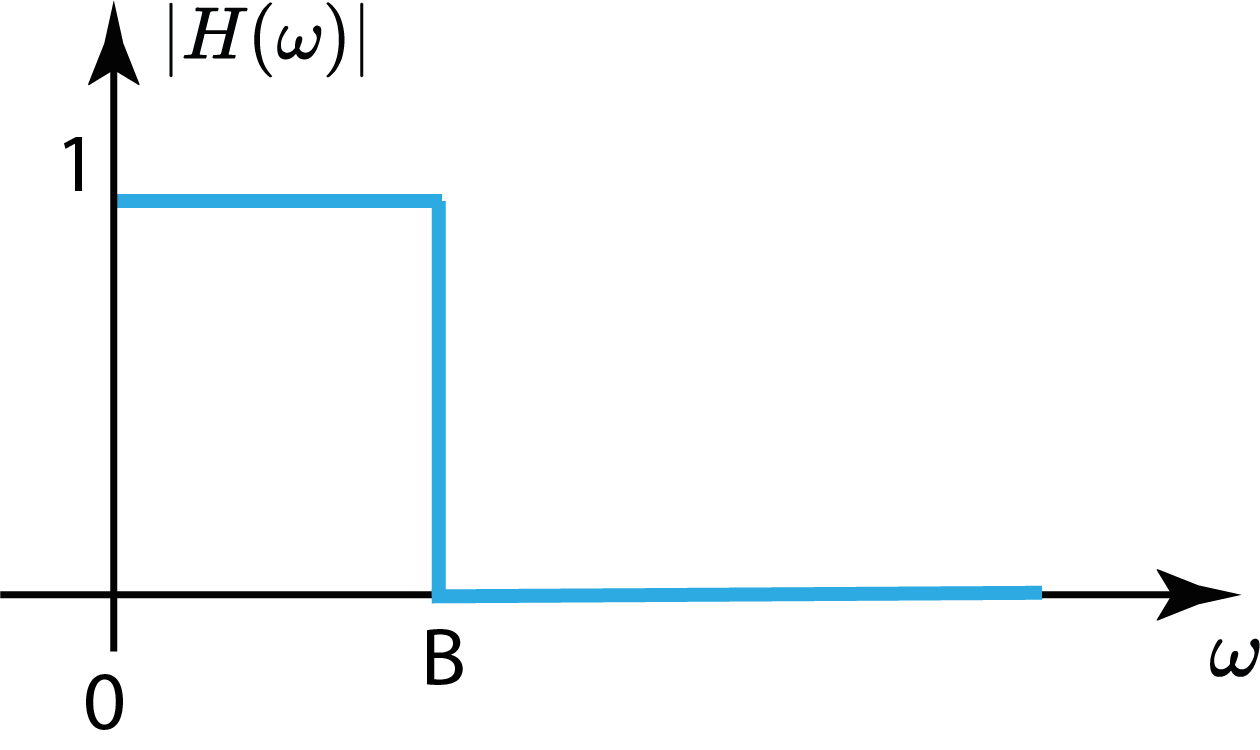
Filtros Passa Alta
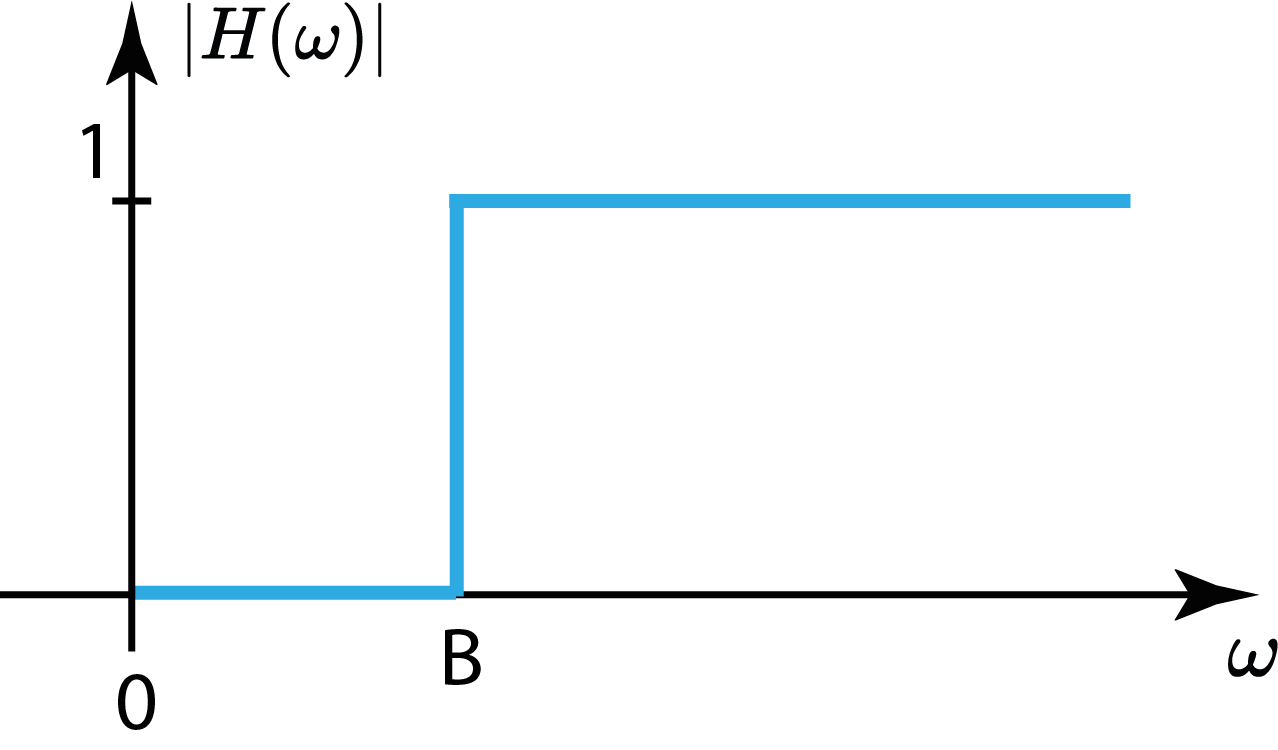
Filtros Passa Faixa
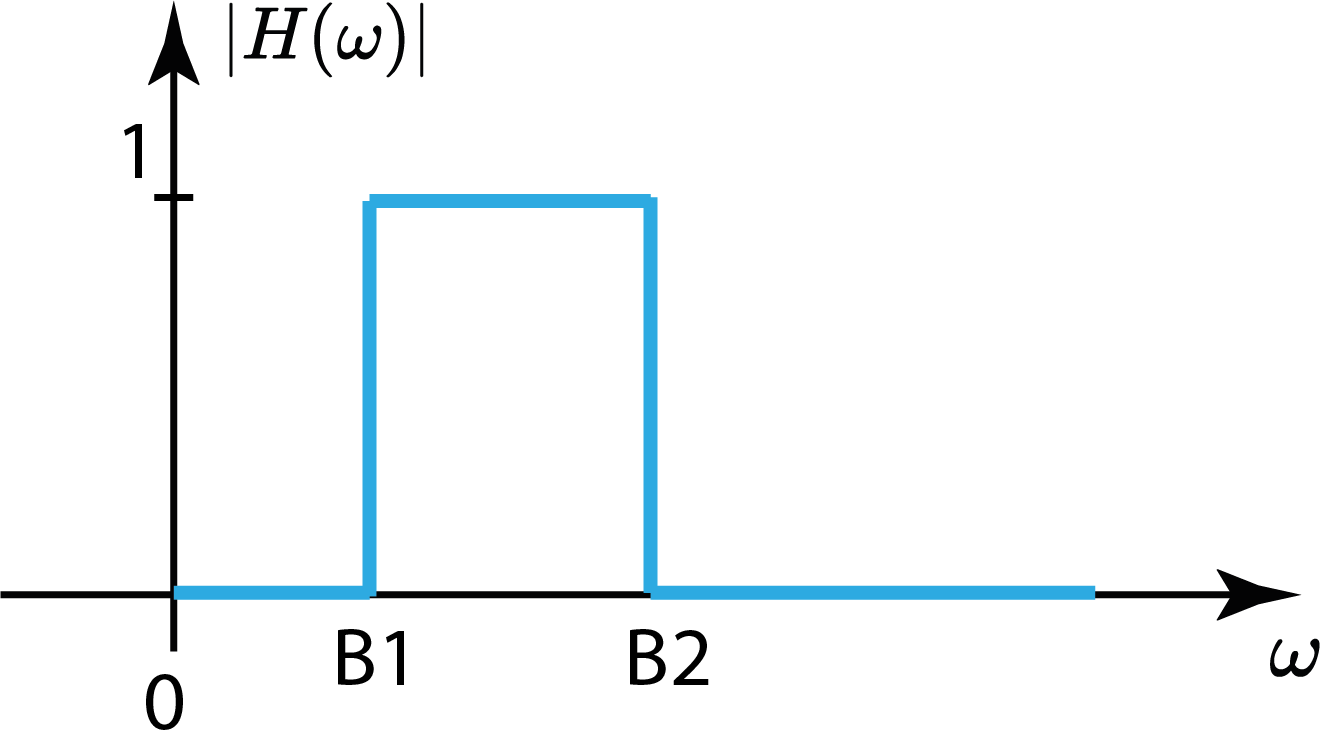
Filtros Rejeita Faixa
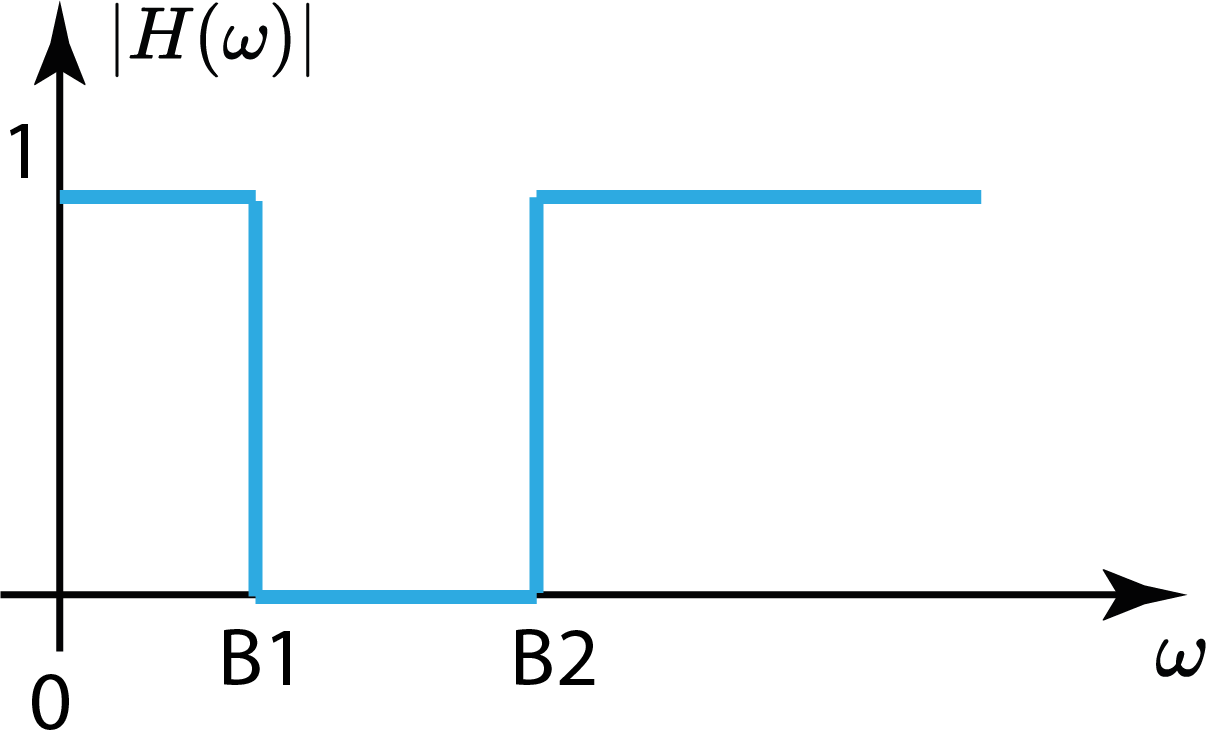
Objetivos
- Filtro Analógico Passa Baixa RC
- Filtro Analógico Passa Alta RL
- Filtros Analógico Passa-Faixa RLC
- Filtros Analógico Rejeita-Faixa RLC
- Exemplos.
Divisor de tensão
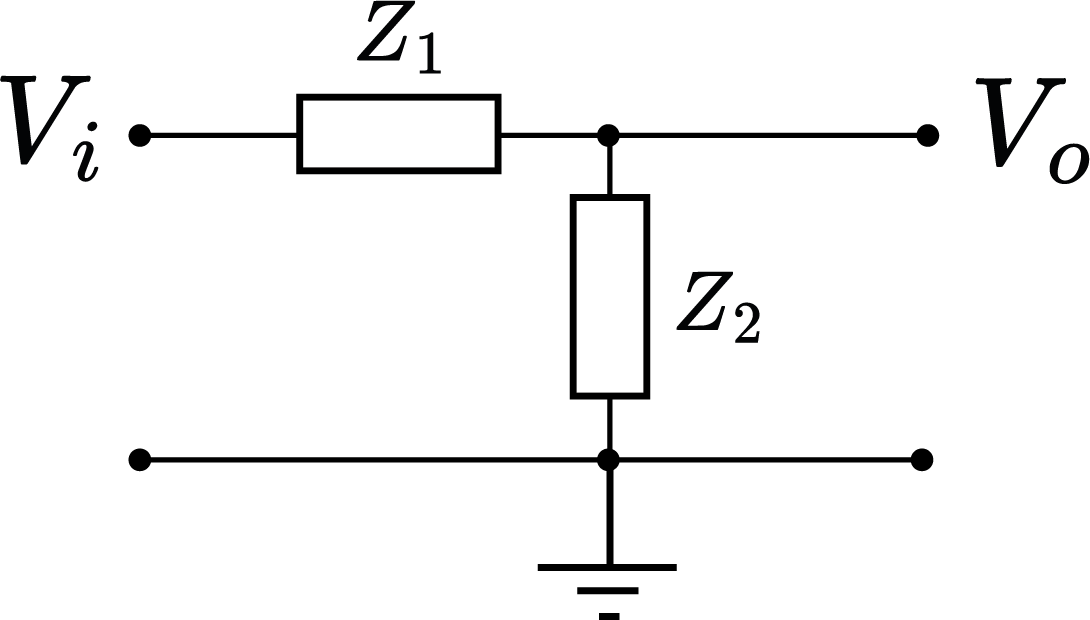
$ V_o(\omega)=V_i(\omega)\frac{Z_2}{Z_1+Z_2} $
Impedância do Resistor
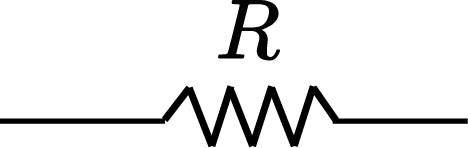
$$ Z_R=R $$
Impedância do Capacitor

$$ Z_C=\frac{1}{j\omega C} $$
Impedância do Indutor
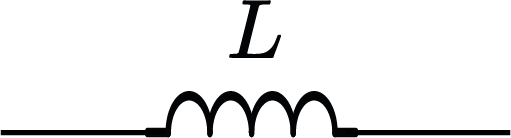
$$ Z_L=j\omega L $$
Impedância
| Resistor | Capacitor | Indutor |
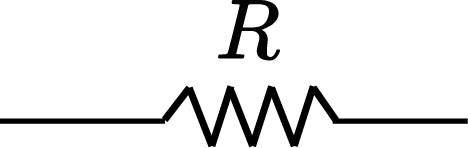 |
 |
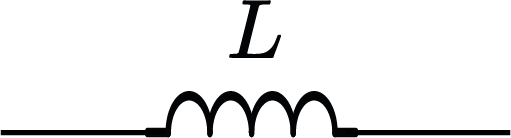 |
| $Z_R=R$ | $Z_C=\frac{1}{j\omega C}$ | $Z_L=j\omega L$ |
Filtro Passa-baixa RC
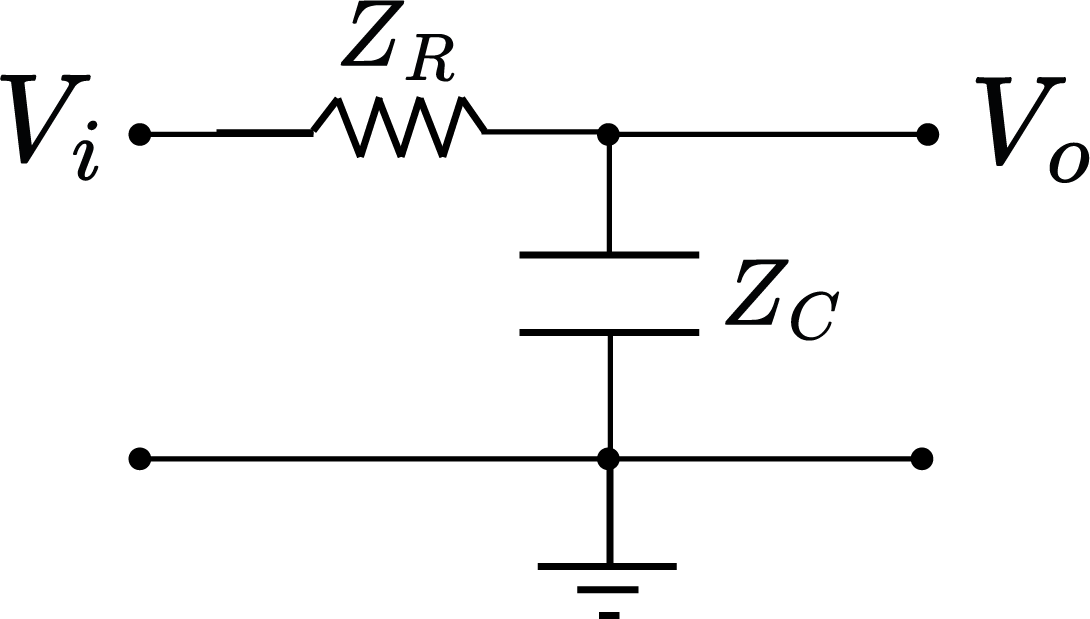
$ H(\omega)=\frac{\frac{1}{RC}}{j\omega+\frac{1}{RC}} $
Filtro Passa-baixa RC
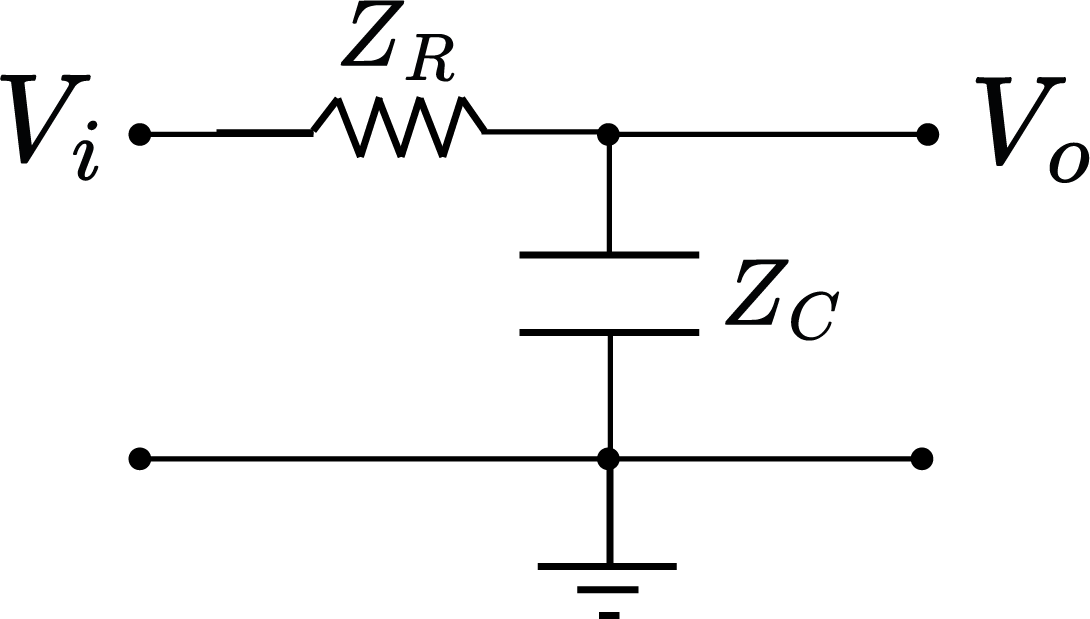
$ |H(\omega)|=\frac{\frac{1}{RC}}{\sqrt{\omega^2+\frac{1}{(RC)^2}}},\quad \theta(\omega)=-\arctan(\frac{\omega}{RC}) $
Filtro Passa-baixa RC
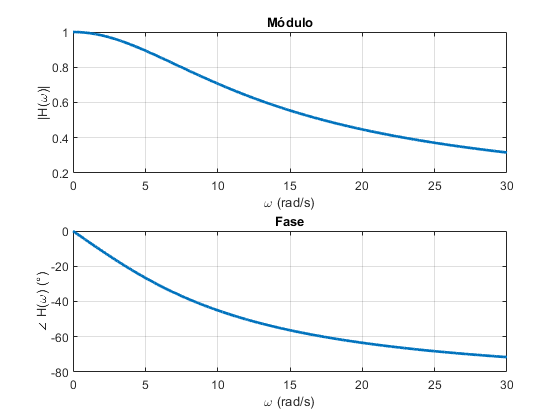
Módulo em dB
Filtro Passa-baixa RC (Diagrama de Bode)
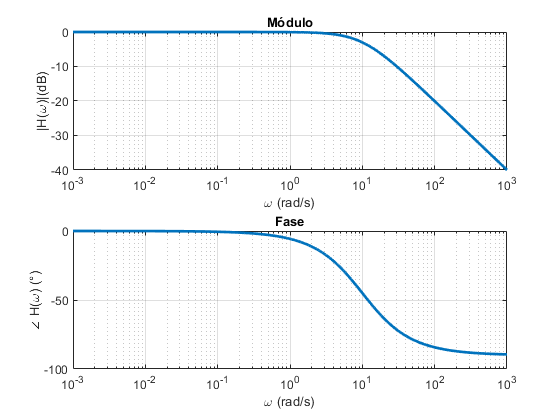
Frequência de corte
$$ |H(\omega)|^2\to \text{densidade de potência} $$
Frequência de corte
Meia-potência $$ |H(B)|^2=\frac{1}{2} $$
$\Rightarrow B$ é a frequência de corte do filtro.
Frequência de corte
Meia-potência $$ |H(B)|=\frac{1}{\sqrt{2}} $$
$\Rightarrow B$ é a frequência de corte do filtro.
Frequência de corte
Meia-potência $$ |H(B)|_{dB}=20\log_{10}(\frac{1}{\sqrt{2}})\approx -3dB $$
$\Rightarrow B$ é a frequência de corte do filtro.
Filtro Passa-baixa RC (Diagrama de Bode)
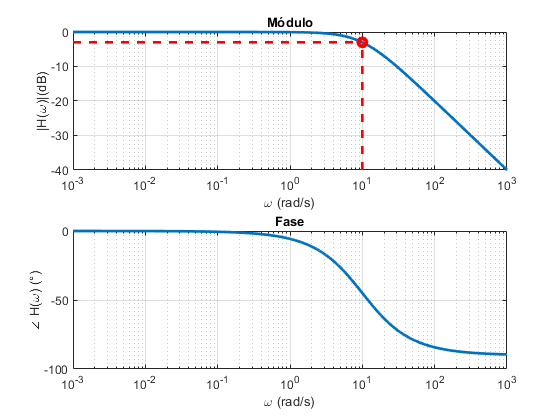
Filtro Passa-baixa RC (Diagrama de Bode)
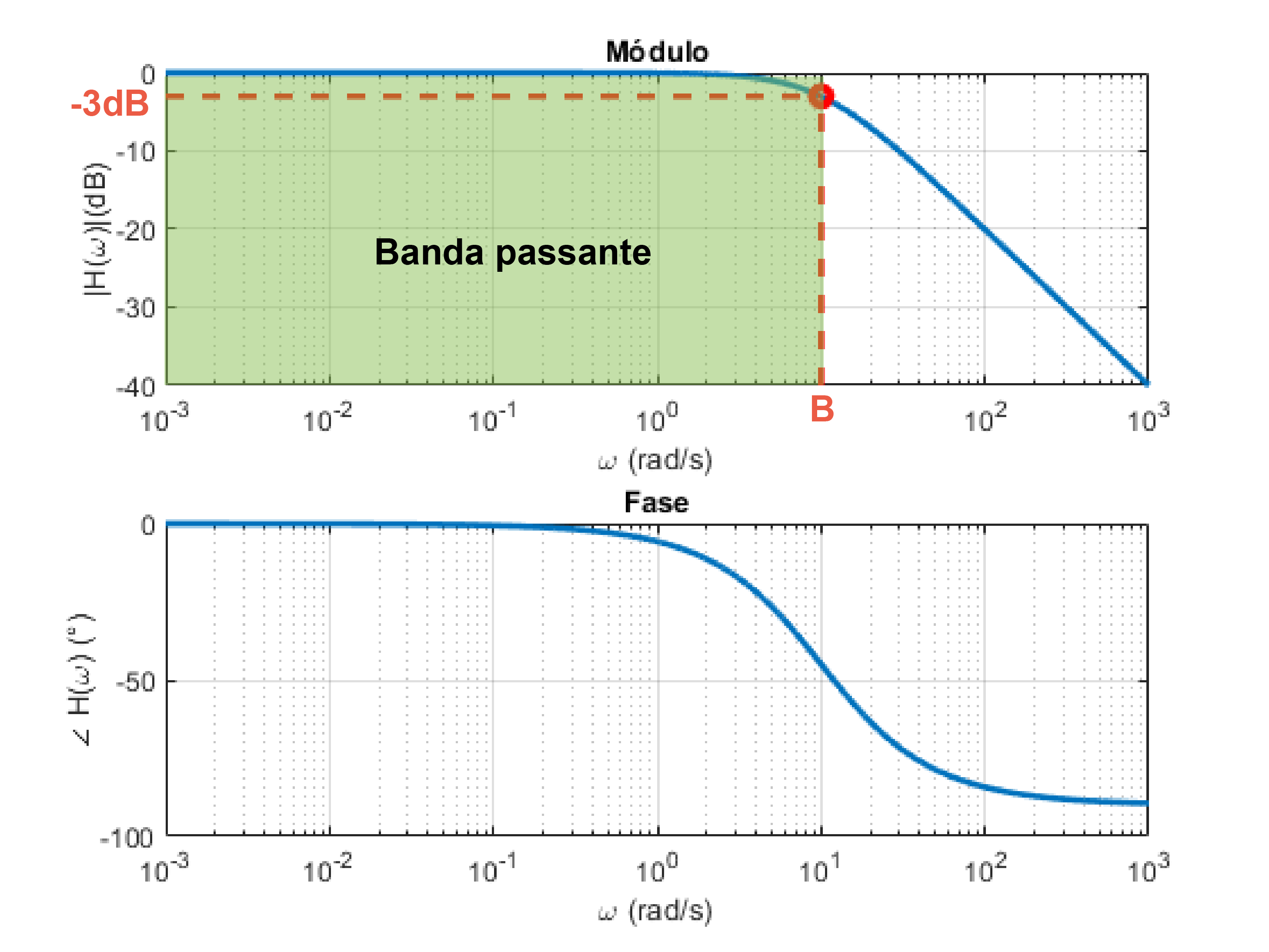
Frequência de corte (B) p/ filtro RC
Filtro Passa-baixa RC
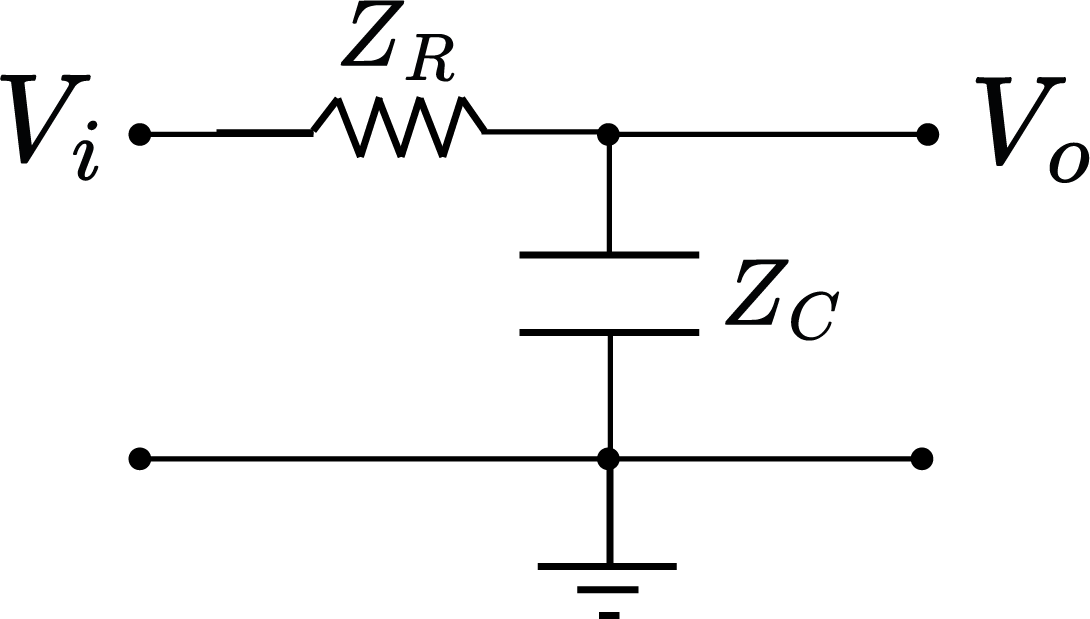
Exemplo:
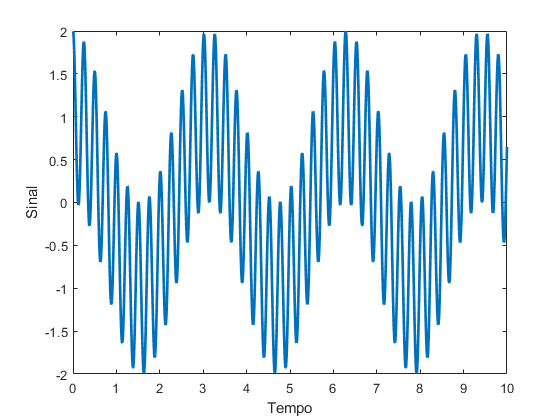
Exemplo:
$ B\approx 3 rad/s $
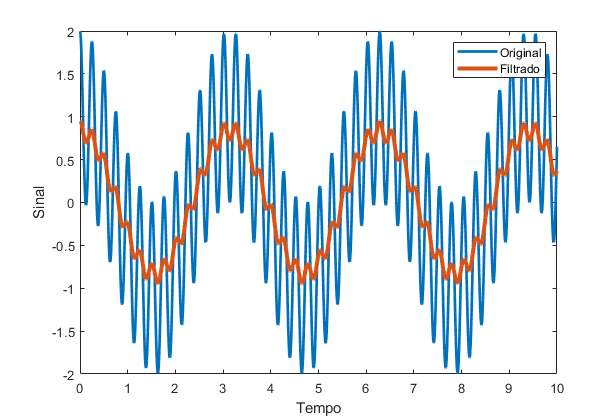
Exemplo:
$ B\approx 3 rad/s $
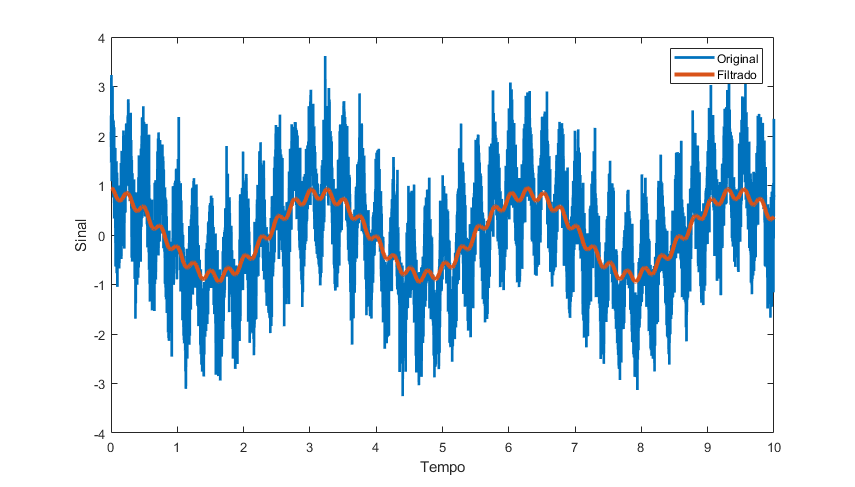
Filtro Passa-Alta RL
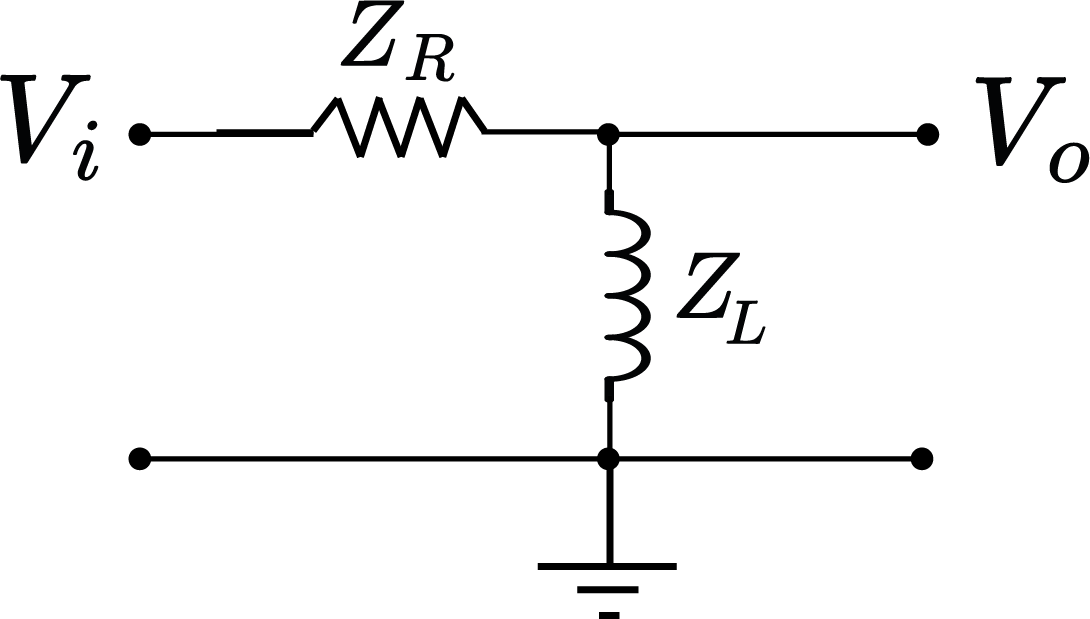
Filtro Passa-Alta RL
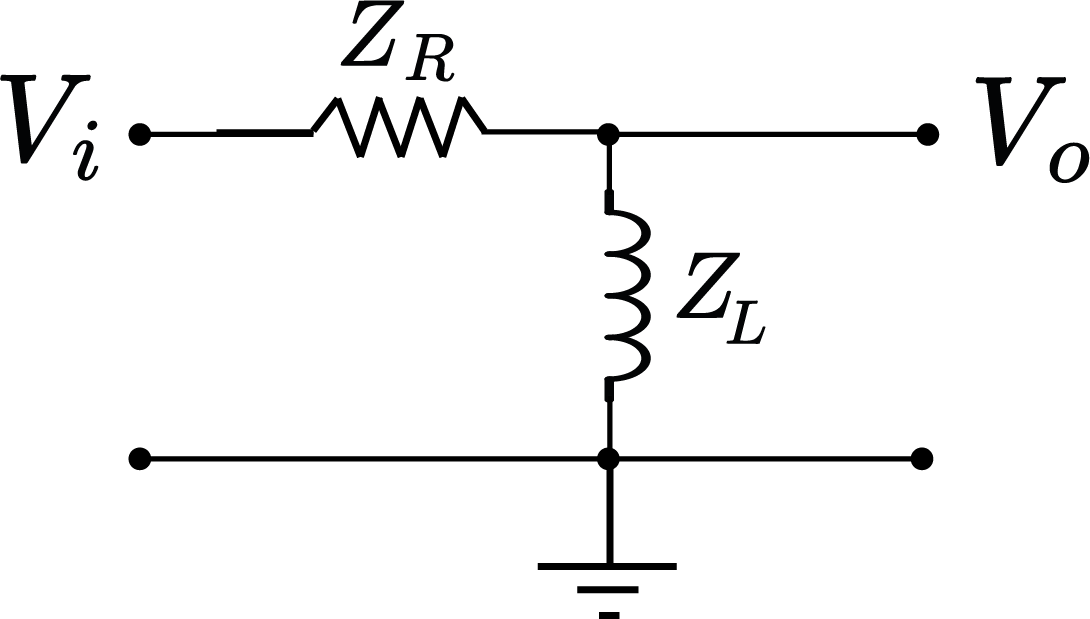
Filtro Passa-Alta RL
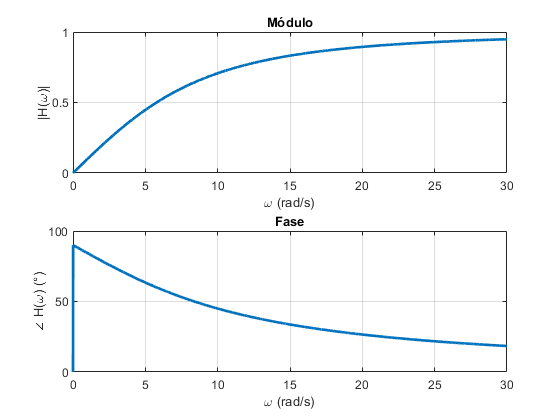
Filtro Passa-Alta RL (Diagram de Bode)
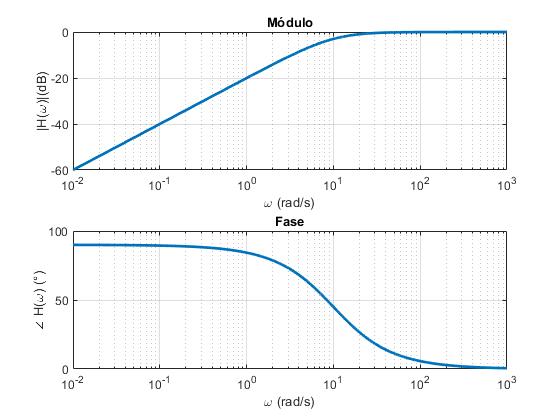
Filtro Passa-Alta RL (Diagram de Bode)
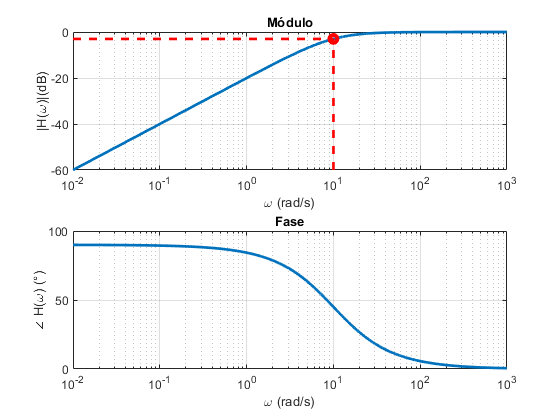
Filtro Passa-Alta RL (Diagram de Bode)
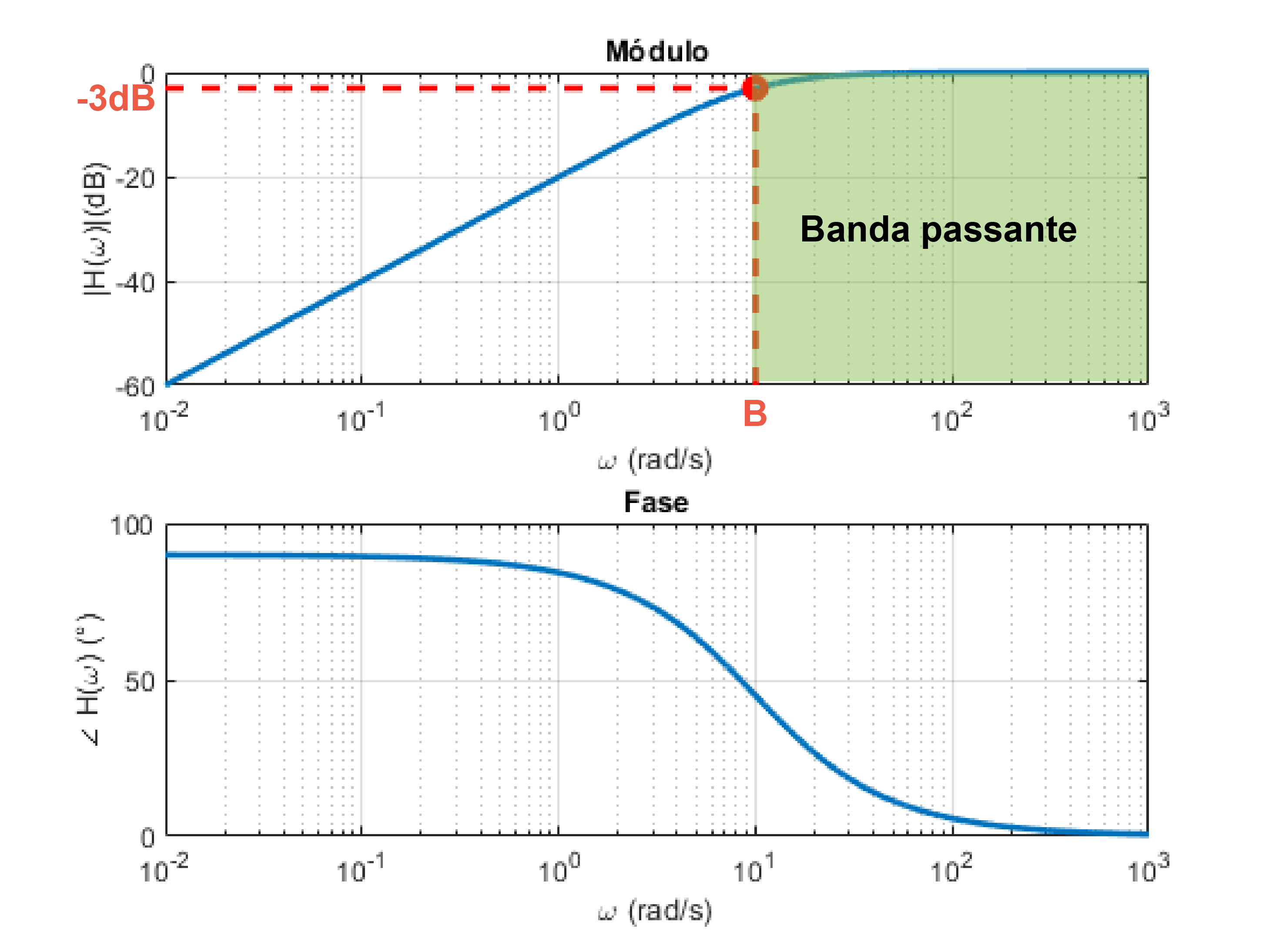
Frequência de corte (B) p/ filtro RL
Filtro Passa-Alta RL
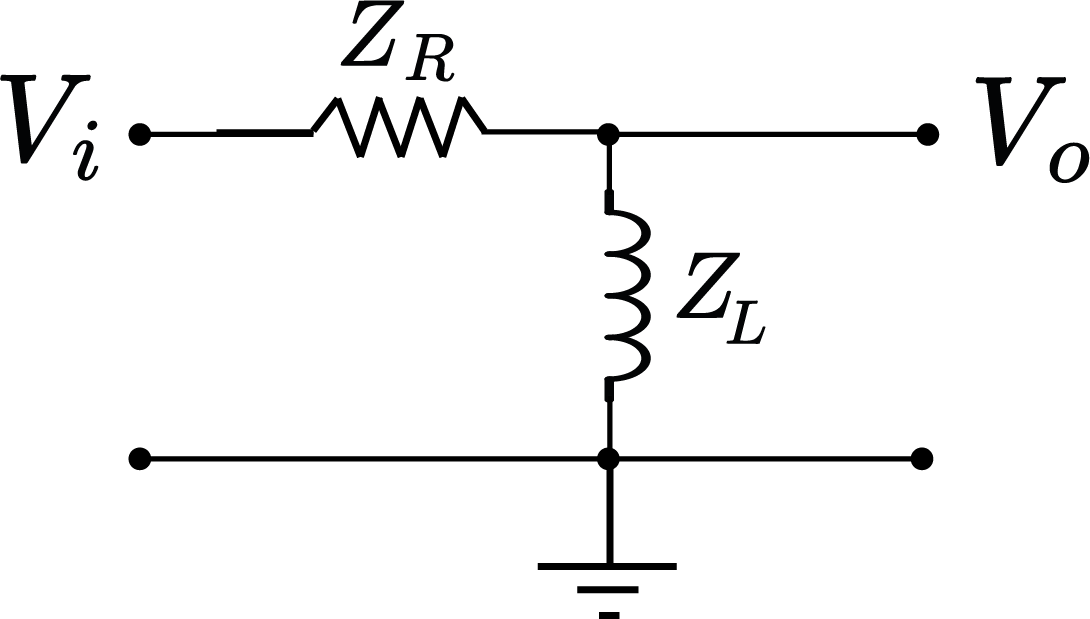
Filtro Passa-Faixa RLC
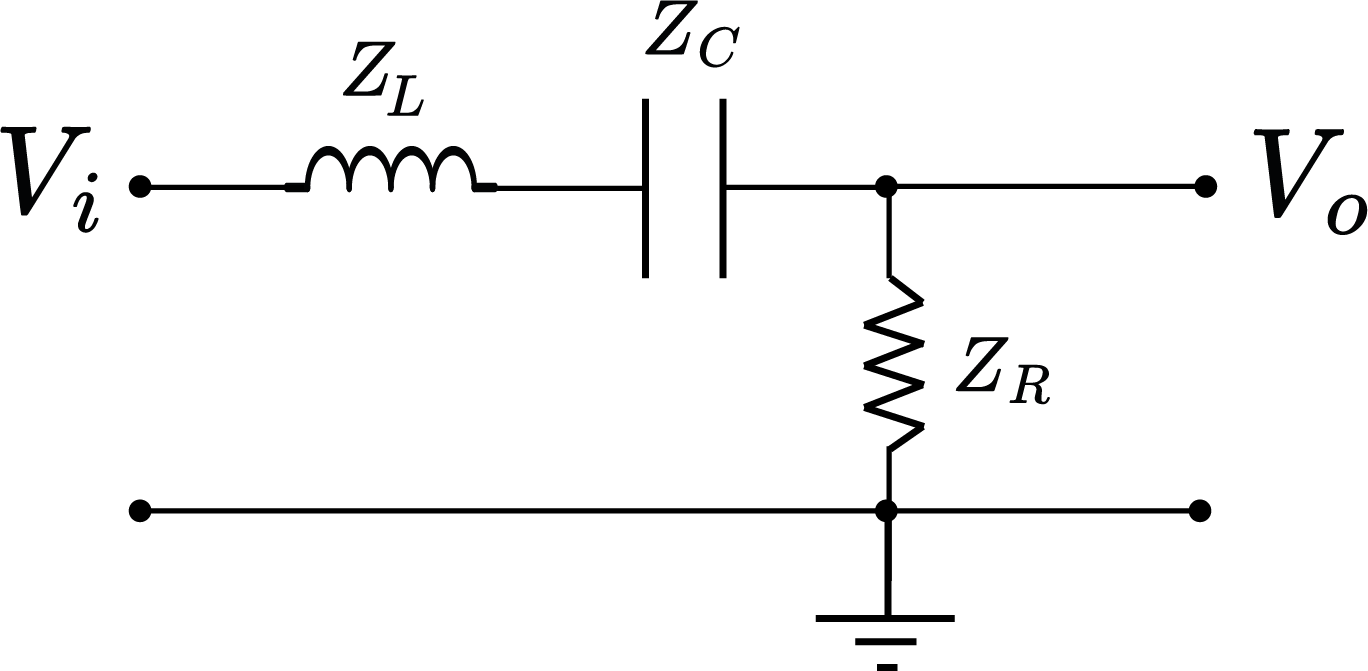
Filtro Passa-Faixa RLC
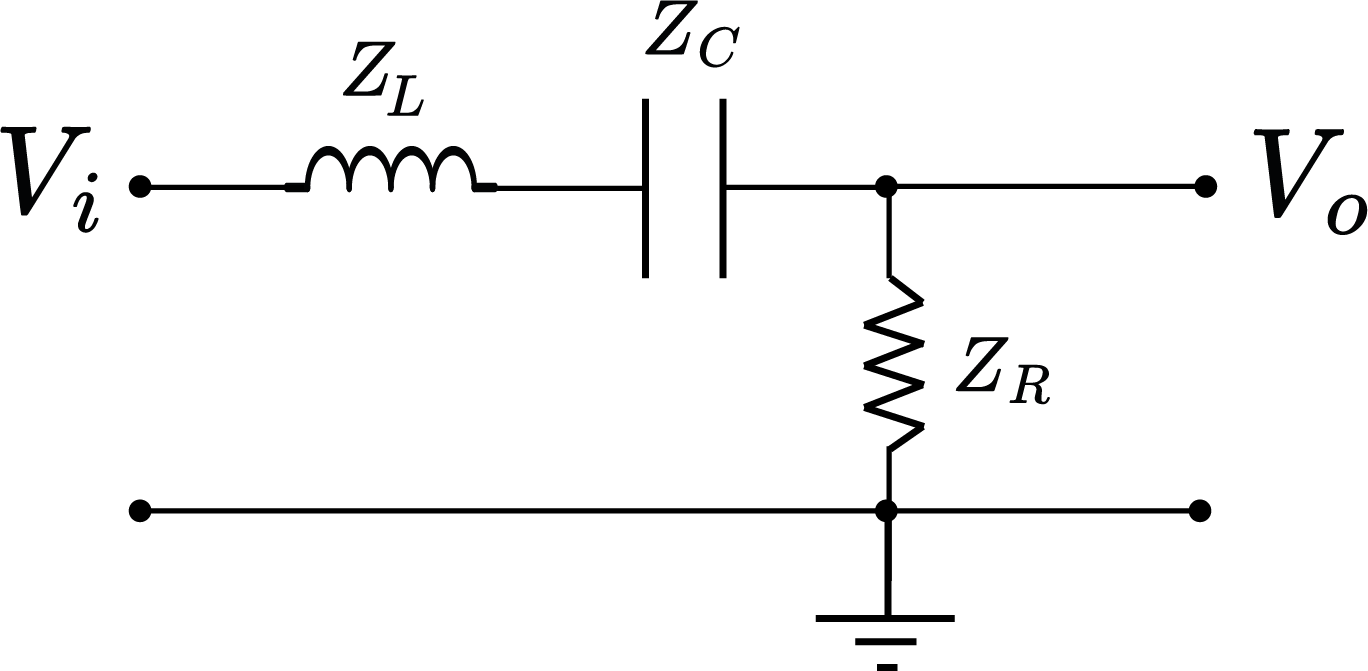
Filtro Passa-Faixa RLC (Diagrama de Bode)
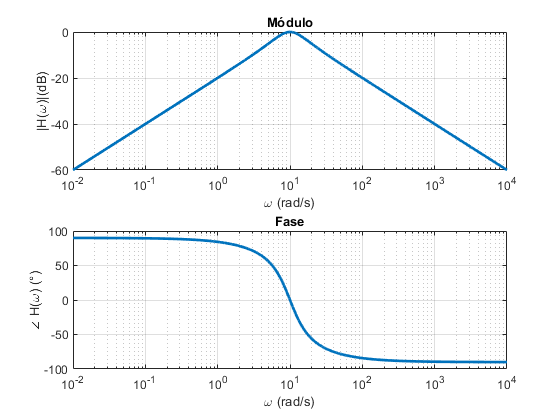
Filtro Passa-Faixa RLC (Diagrama de Bode)
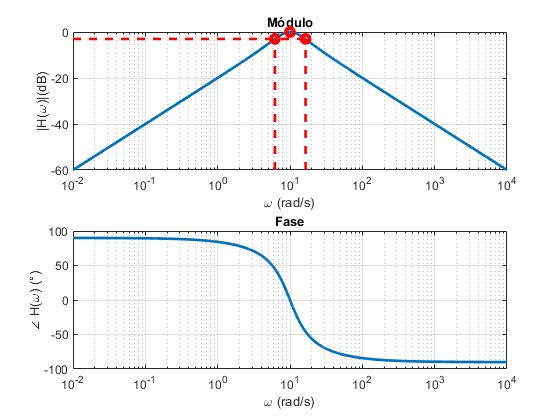
Filtro Passa-Faixa RLC (Diagrama de Bode)
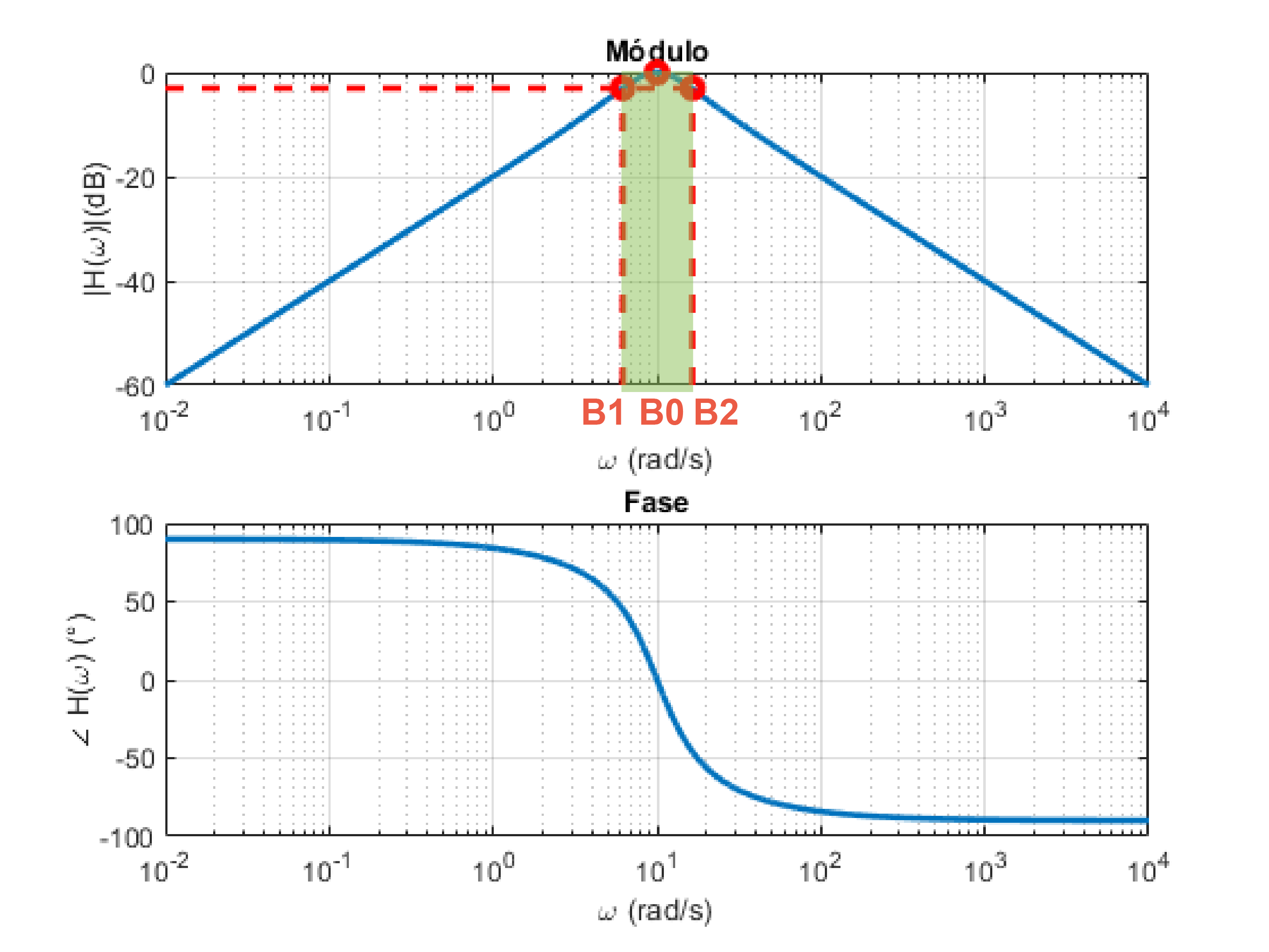
Filtro Rejeita-Faixa RLC
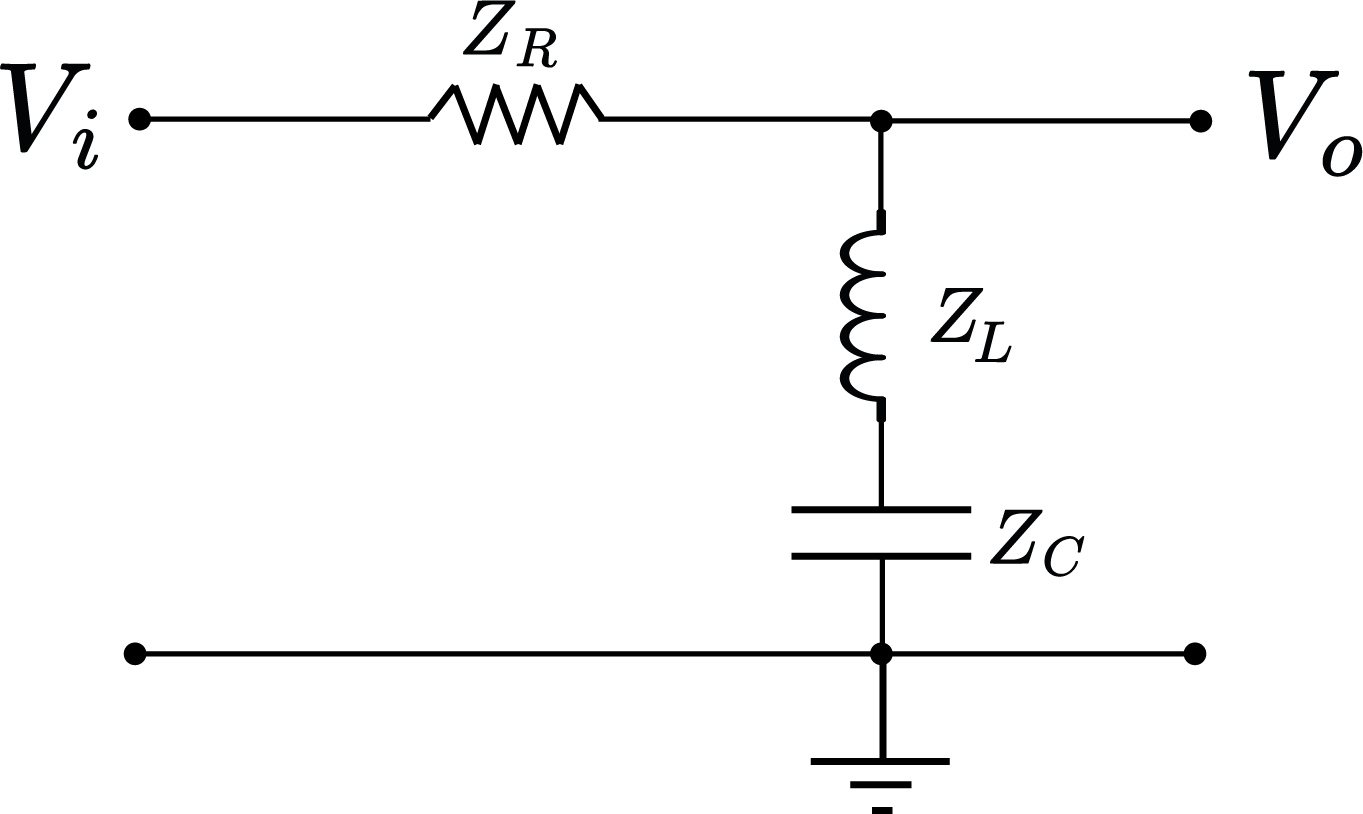
$H(\omega)=\frac{j(\omega L-\frac{1}{\omega C})}{R+j(\omega L-\frac{1}{\omega C})}$
Filtro Rejeita-Faixa RLC
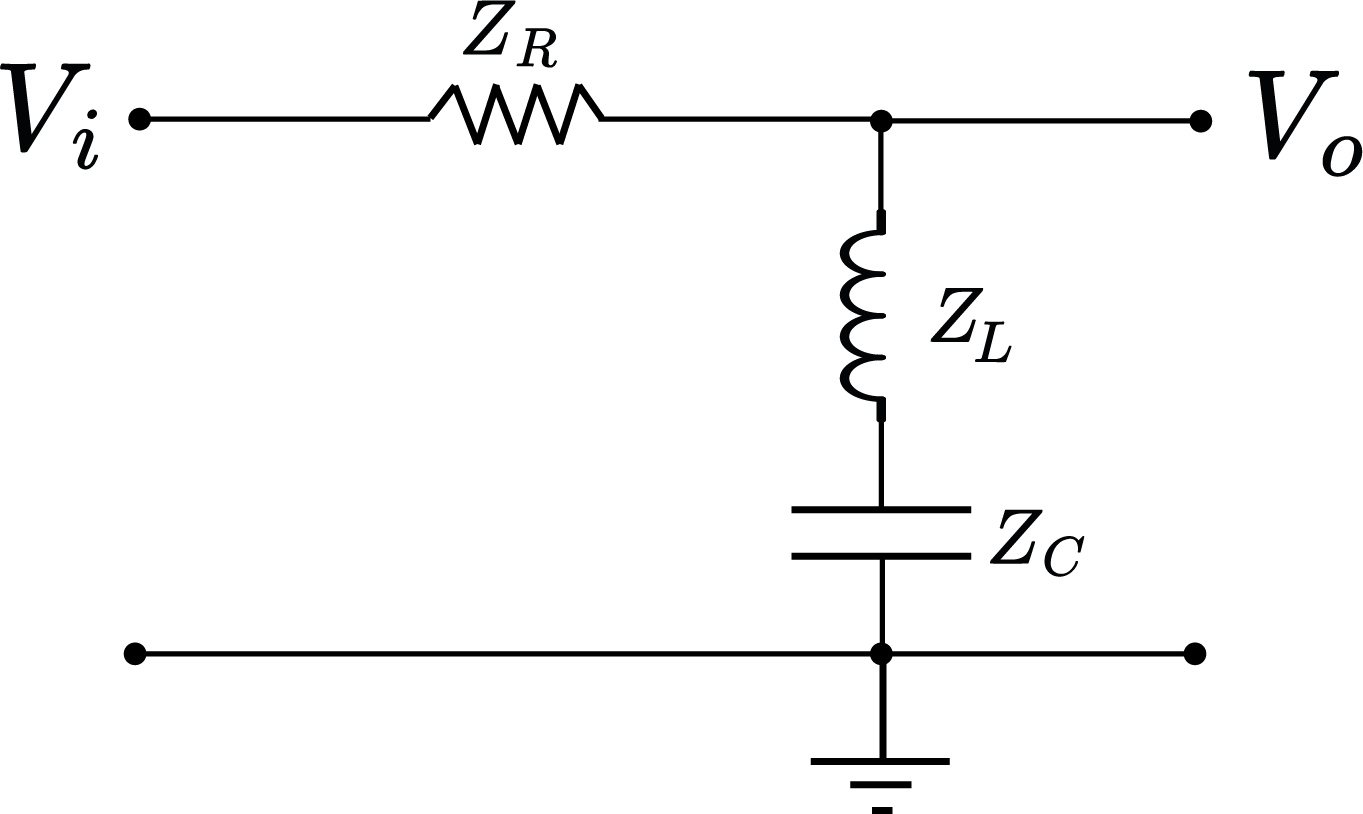
$B_0=\frac{1}{\sqrt{LC}}$
Filtro Rejeita-Faixa RLC (Diagrama de Bode)
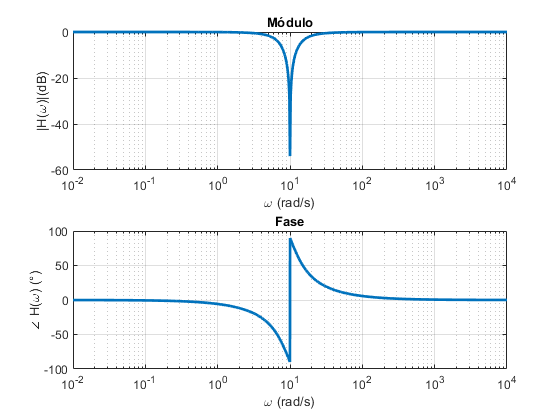
Filtro Rejeita-Faixa RLC (Diagrama de Bode)
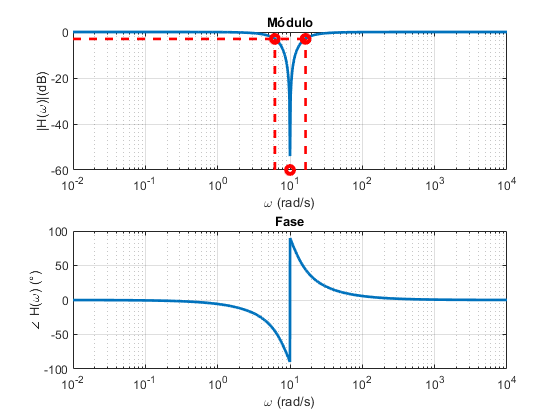
Filtro Rejeita-Faixa RLC (Diagrama de Bode)
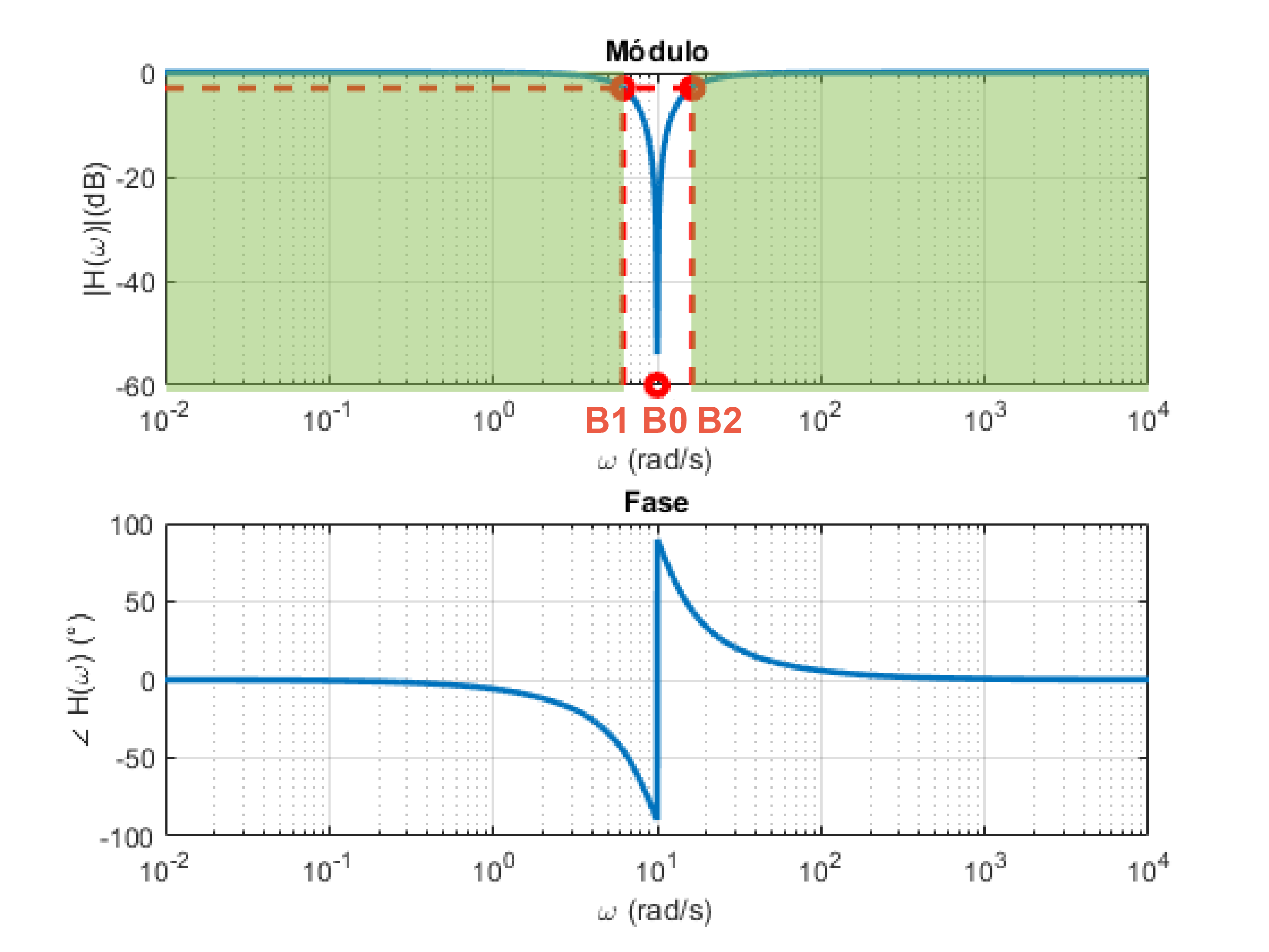
Próxima aula
Filtros Analógicos - parte 2