

Aula 15:
Introdução à análise de sistemas
SEL0604
Prof. Marcos Rogério Fernandes
21 de outubro de 2024
Objetivos
Os objetivos dessa aula são entender:
- Definição de sistemas;
- Propriedades de sistemas;
- Classificações de sistemas;
- Sistemas Lineares Invariantes no Tempo
- Exemplos
Sinais
Sinal é tudo que carrega informação.
Sistemas
O que é um sistema?
Sistema é tudo que modifica um sinal.
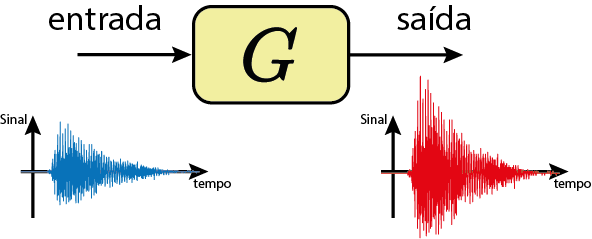
Exemplos de sistemas
Telecomunicações

Internet
Indústria: variáveis de processo

Corpo Humano
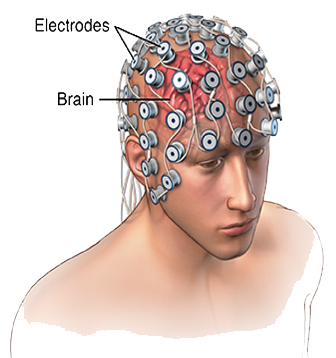
Corpo Humano
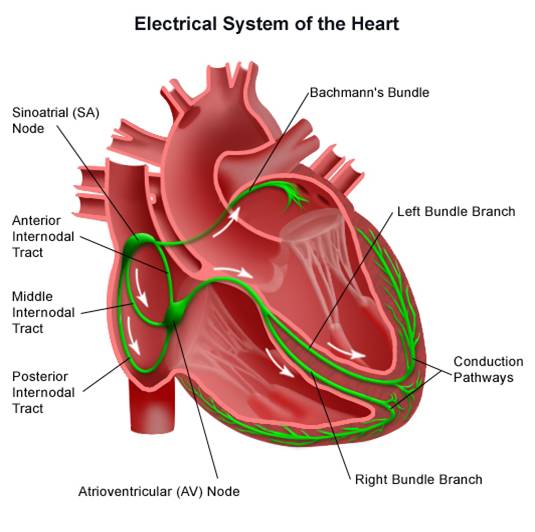
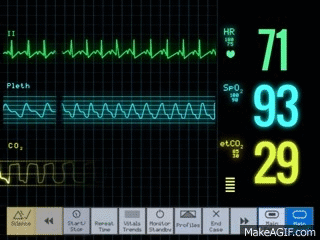
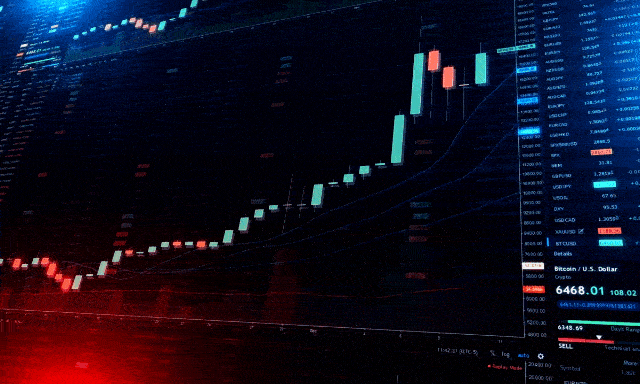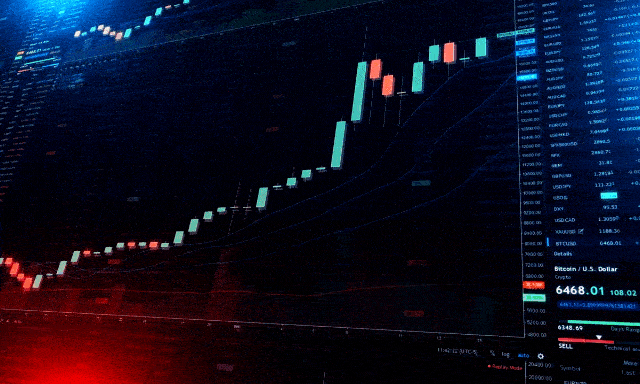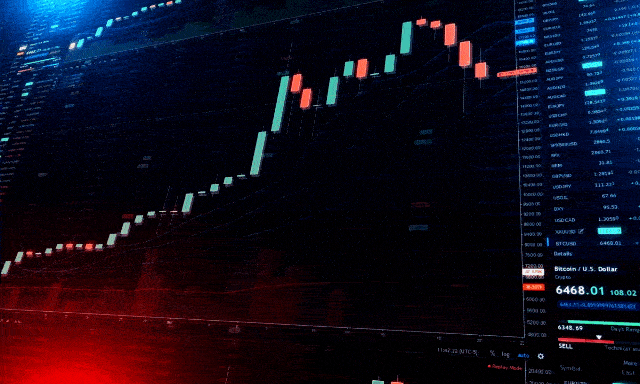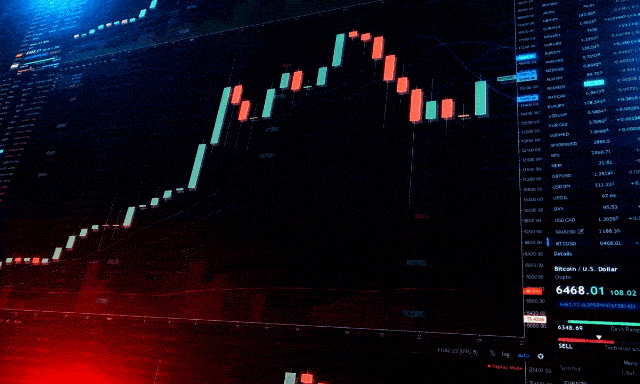
Mercado Financeiro
Representação matemática
Função matemática $g:\mathbb{R}\to\mathbb{C}$

Os mesmos conceitos são validos para dimensões maiores
($\mathbb{R}^2,\mathbb{R}^3$,...$\mathbb{R}^n$)
Representação matemática
Função matemática?
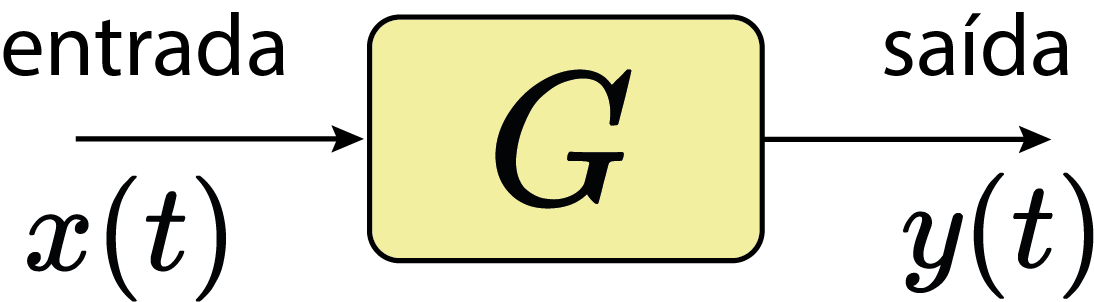
Sistema
Representação matemática
Operador que transforme um sinal em outro sinal!
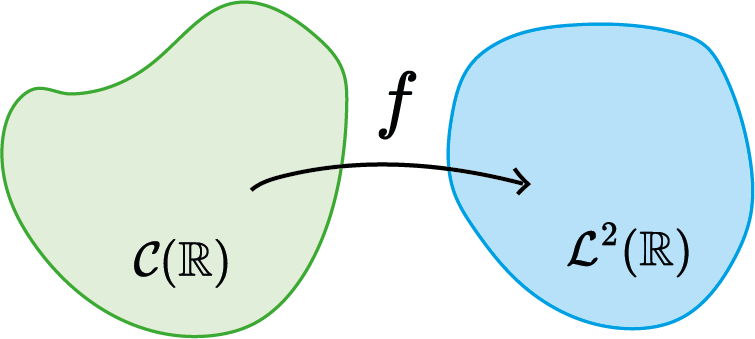
Equações Diferenciais Ordinárias (EDO)
Representação matemática
EDO
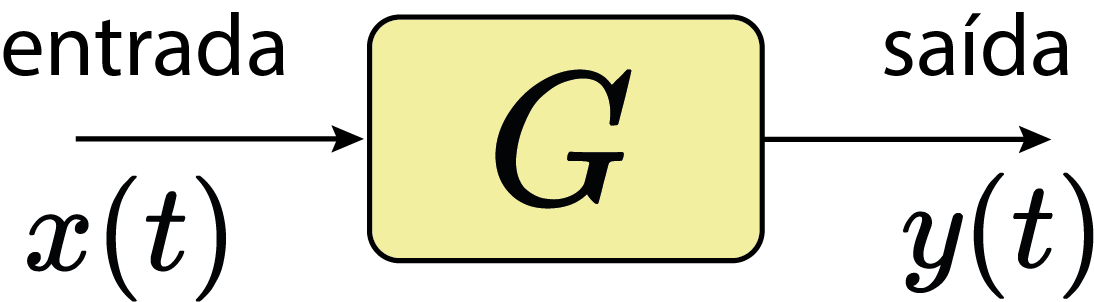
Sistema
$$ y(t)=G\{x(t)\} $$
Propriedades dos sistemas
- Linearidade
- Invariância temporal;
- Memória;
- Causalidade;
- Estabilidade;
Linearidade
Se $$ y_1(t)=G\{x_1(t)\},\quad y_2(t)=G\{x_2(t)\} $$ então, $$ G\{\alpha x_1(t)+\beta x_2(t)\}=\alpha y_1(t) + \beta y_2(t) $$
Invariância Temporal
Se $$ y(t)=G\{x(t)\}, $$ então, $$ G\{x(t-t_0)\}=y(t-t_0) $$
Memória
$$ y(t)=G\{x(t)\}, $$
Causalidade
$$ y(t_0)=G\{x(t)\}, t\le t_0 $$
Estabilidade
BIBO-Estabilidade (Bounded-Input-Bounded-Output):
Se
$$
|x(t)|\le \alpha
$$
então
$$
|y(t)|\le \beta
$$
Estabilidade
BIBO-Estabilidade (Bounded-Input-Bounded-Output):
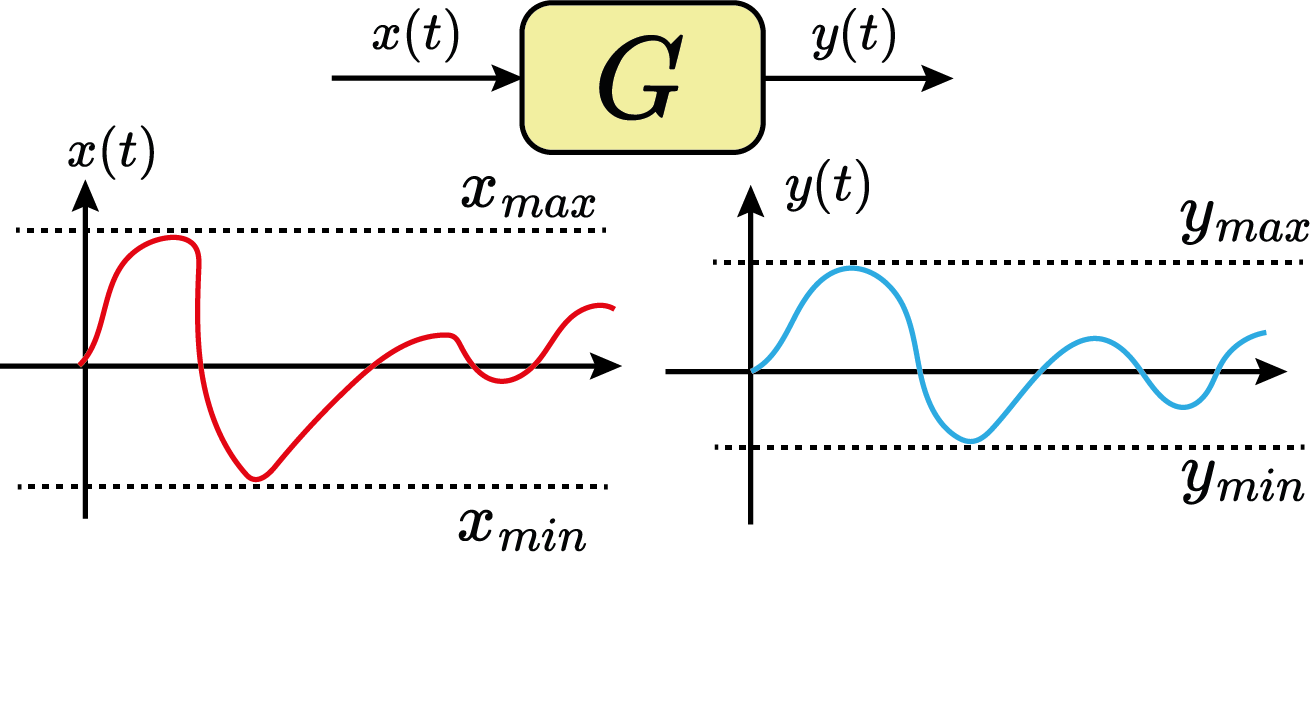
Estabilidade
Estabilidade Assintótica:
$$
\exists \alpha < \infty : \lim_{t\to\infty} |y(t)-\alpha|\to 0
$$
Estabilidade
Estabilidade Assintótica:
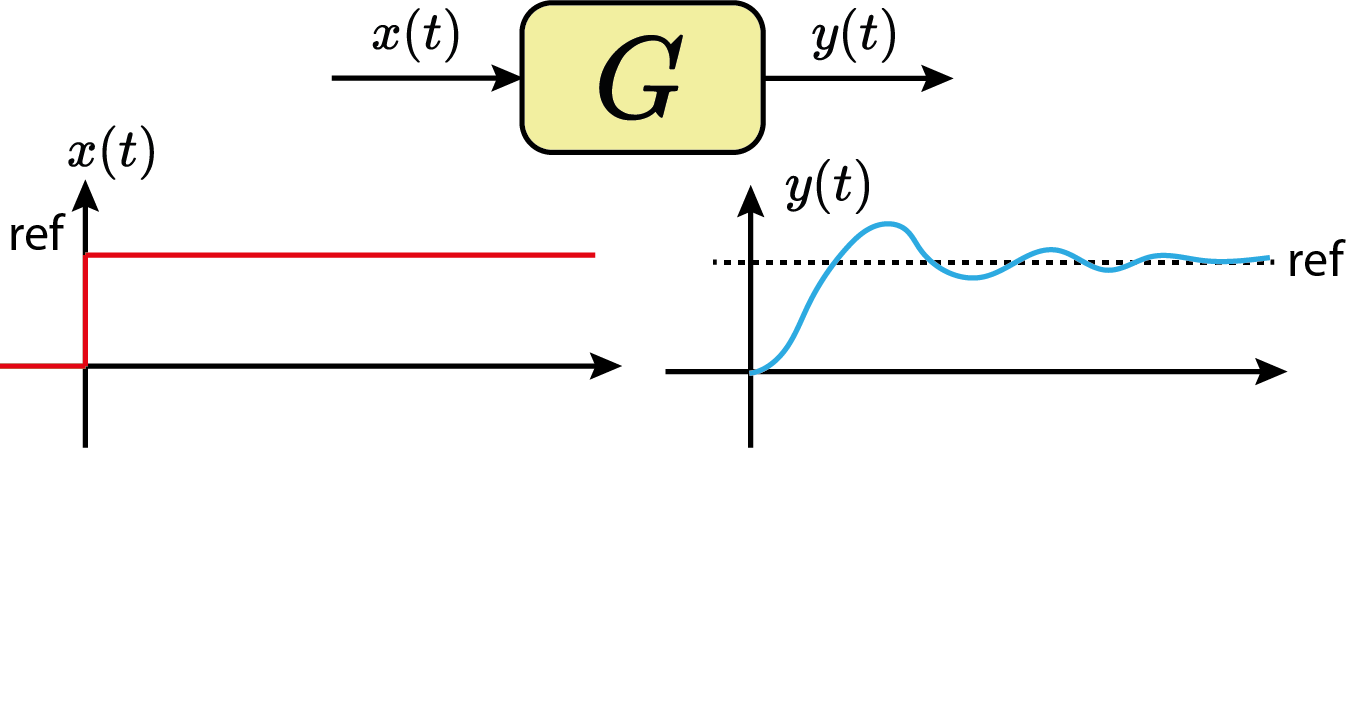
Classificações de sistemas
- Tempo contínuo ou tempo discreto;
- Linear ou Não-linear
- Escalar ou Multivariável;
- Determinísticos ou Estocástico;
- Caótico ou Não-Caótico;
Tempo Contínuo vs Discreto
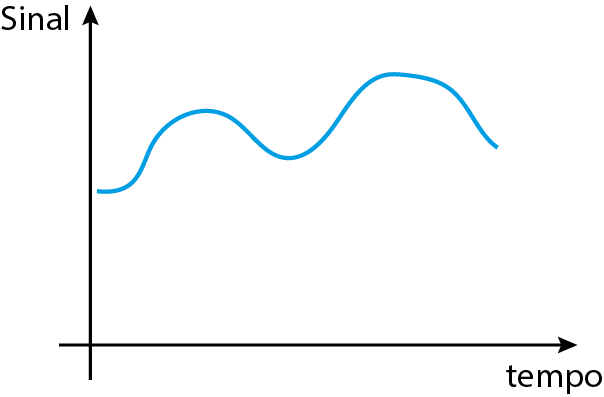
Tempo Contínuo vs Discreto

Tempo Contínuo vs Discreto
Amostragem (Conversão Analógico-para-Digital)
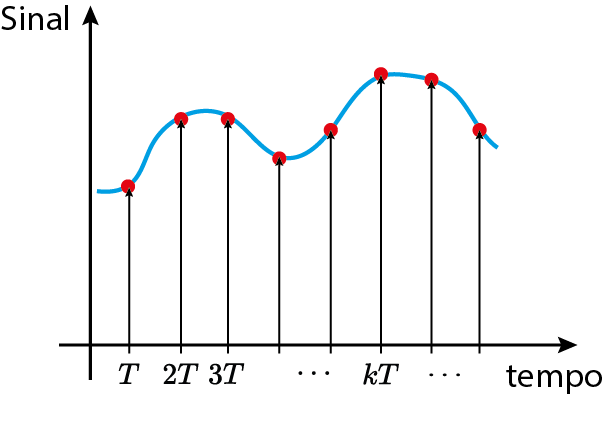
Linear vs Não-linear
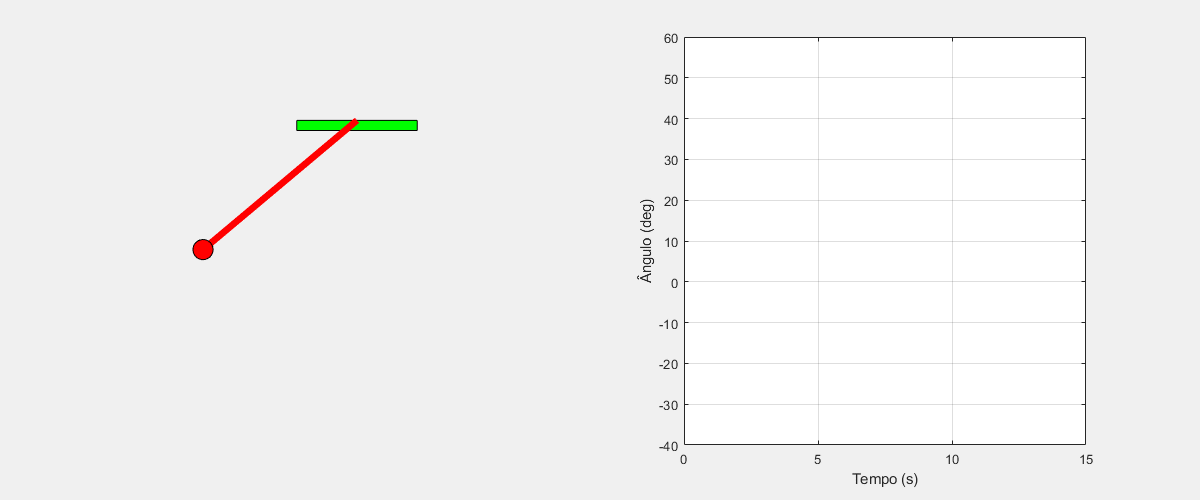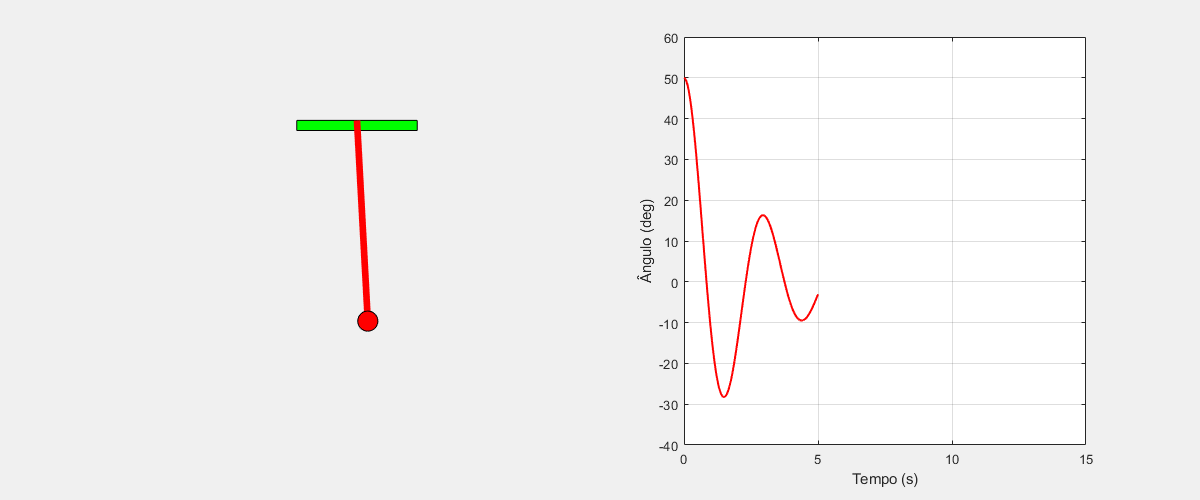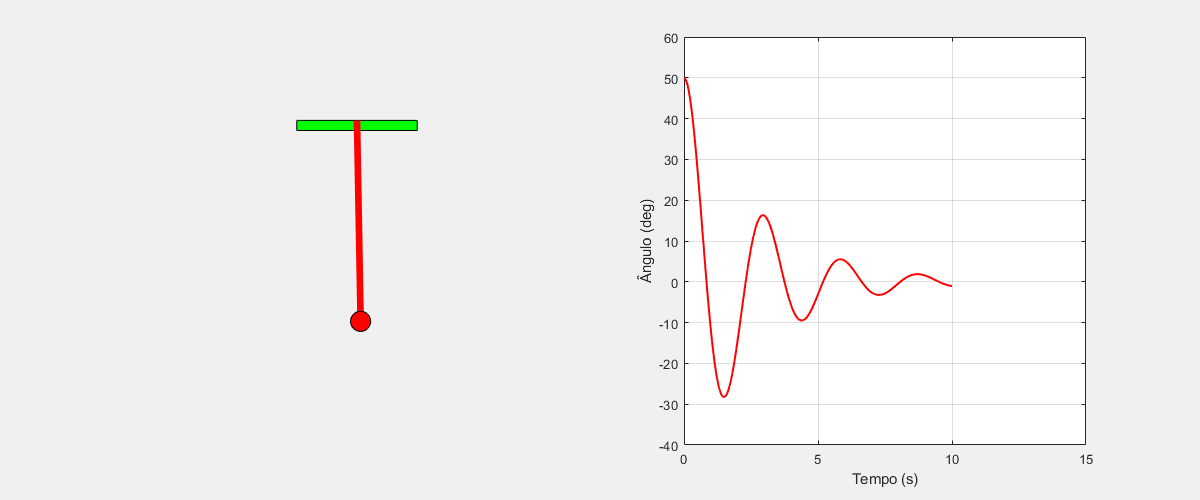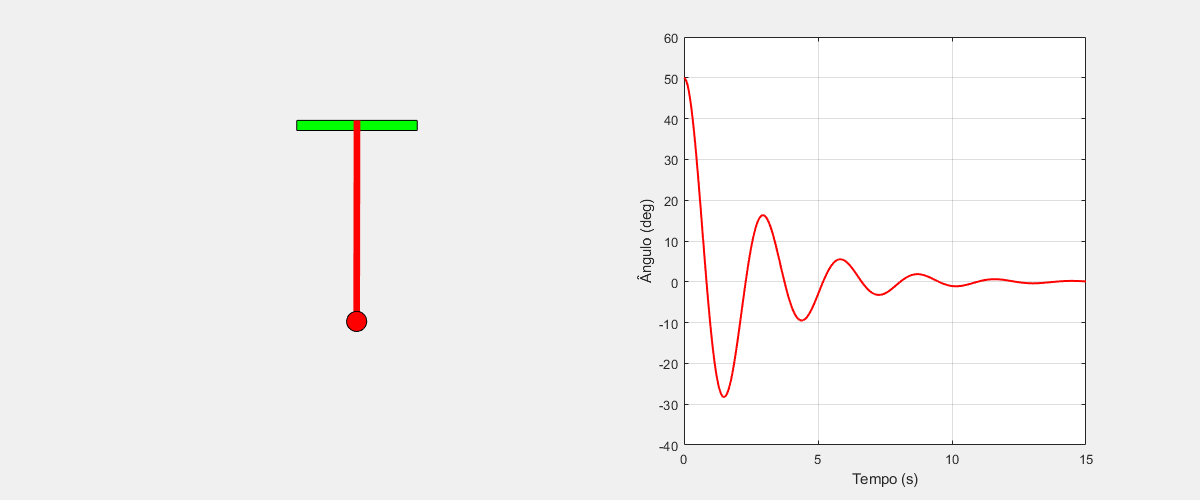
$ l\ddot{\theta}=-g\sin(\theta)-b\dot{\theta}+u $
Linear vs Não-linear
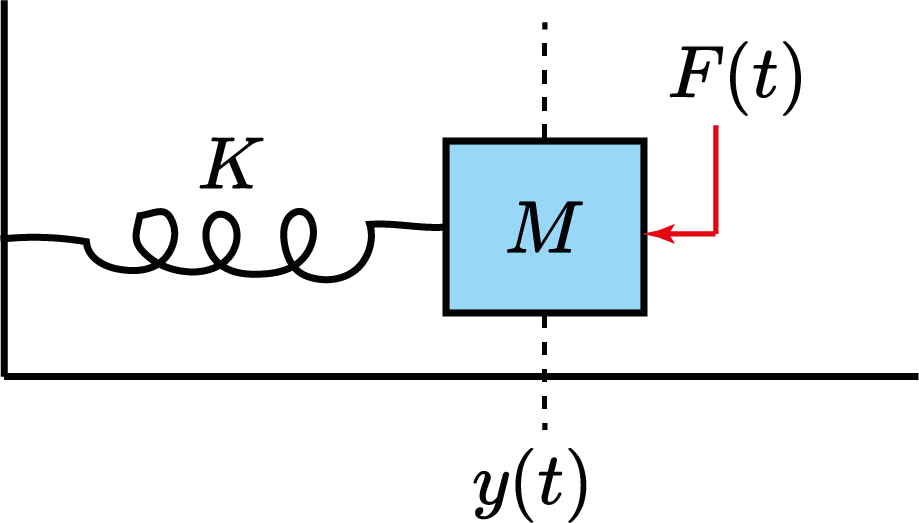
$ \ddot{y}+\alpha \dot{y}+\beta y = F $
Linear vs Não-linear
- Satisfaz propriedade da superposição $\to $ linear
- Não-satisfaz propriedade da superposição $\to$ não-linear
Escalar vs Multivariável
SISO (Single-Input-Single-Output):
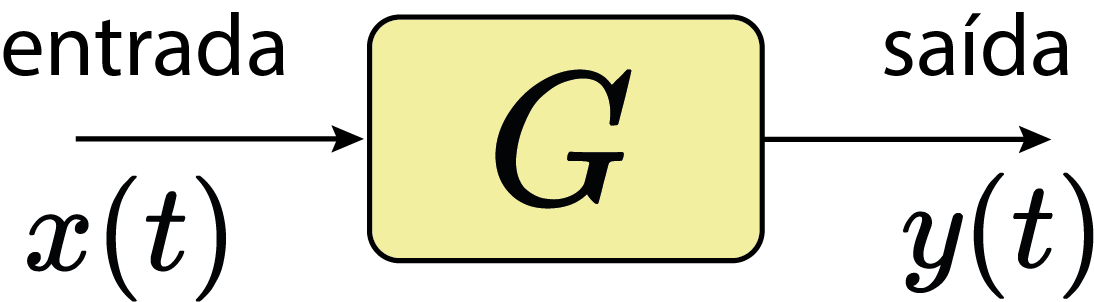
Sistema Escalar (Unidimensional)
$$ x(t)\in\mathbb{R},\quad y(t) \in \mathbb{R} $$
Escalar vs Multivariável
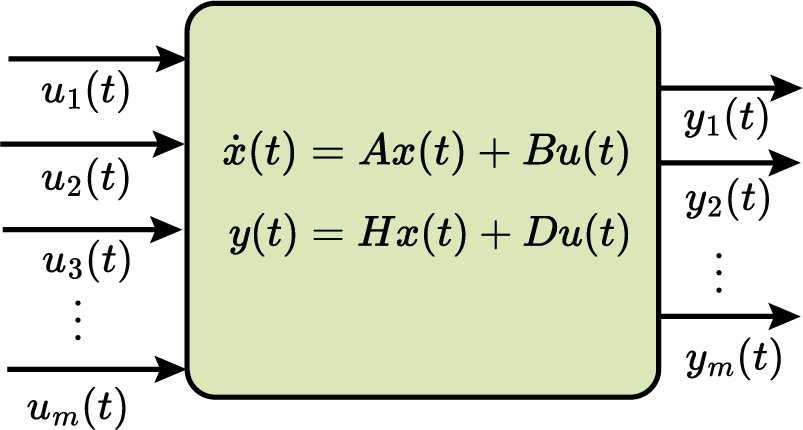
Sistema Multivariável (Multidimensional) $$ u(t)\in\mathbb{R^m},\quad y(t) \in \mathbb{R^p} $$
Determinístico vs Estocástico
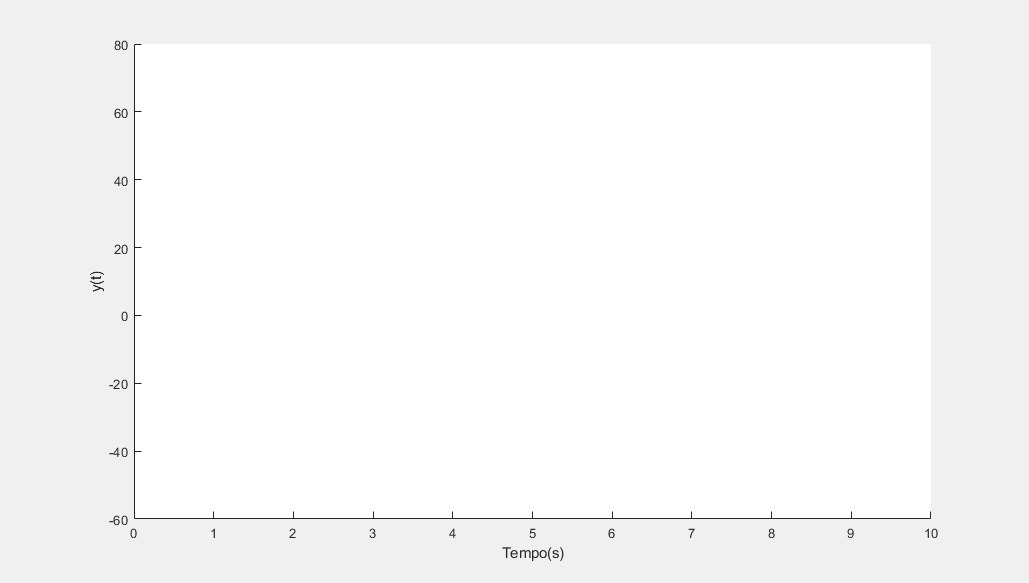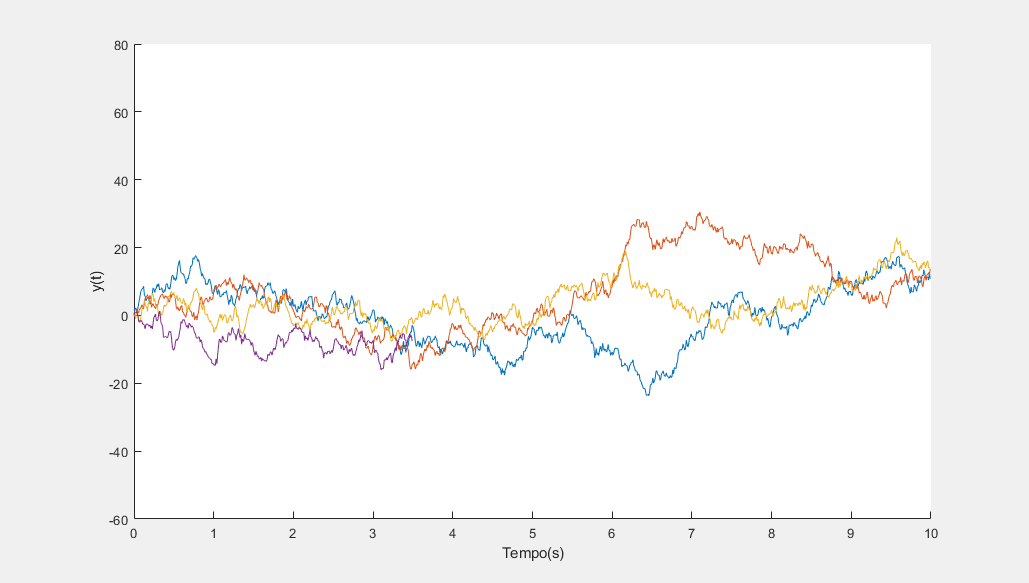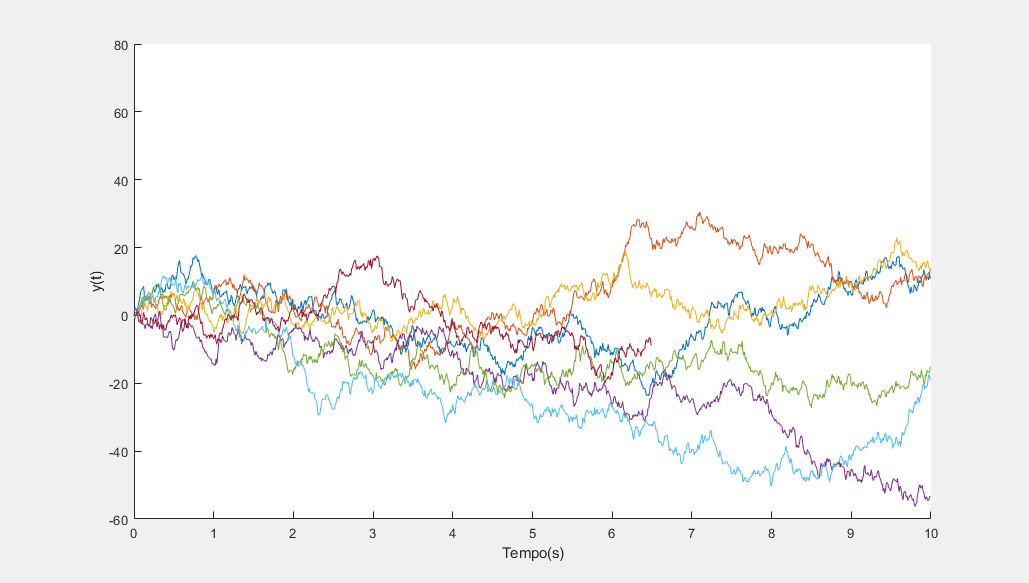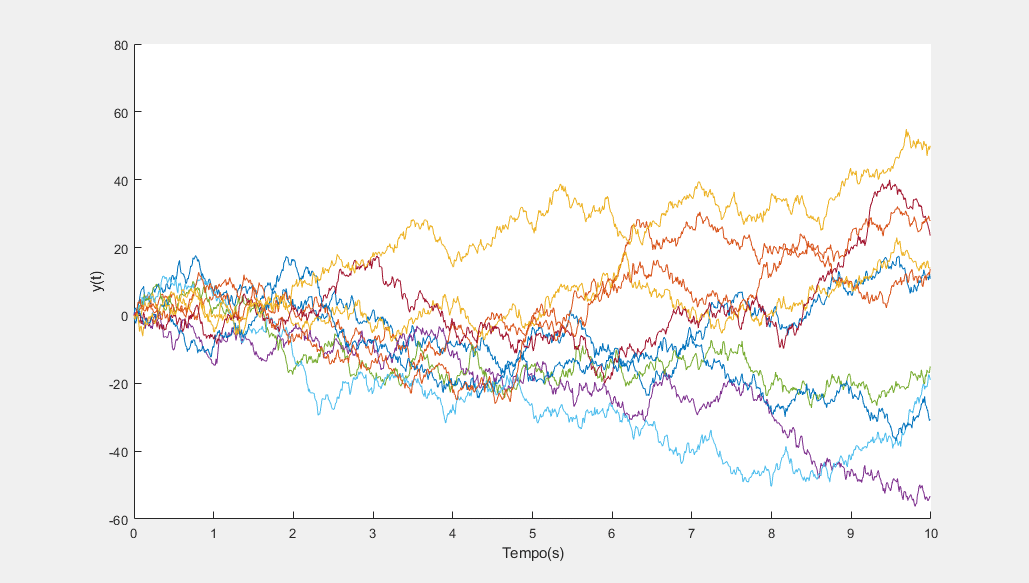
Caótico vs Não-Caótico
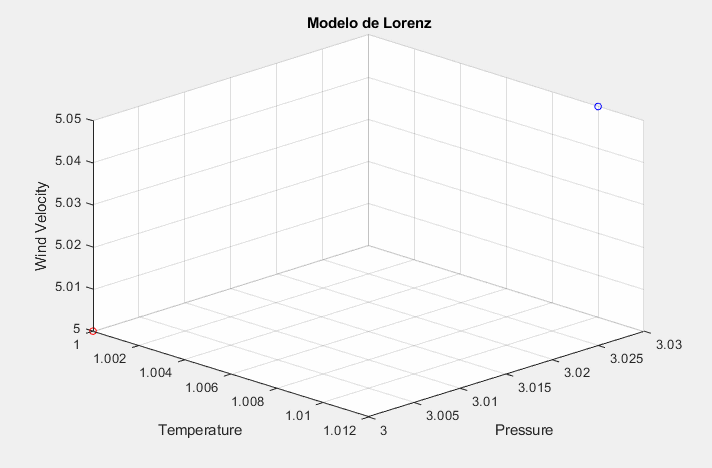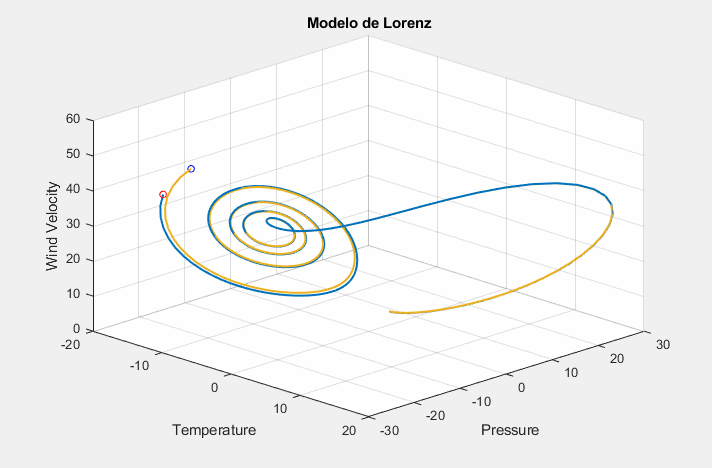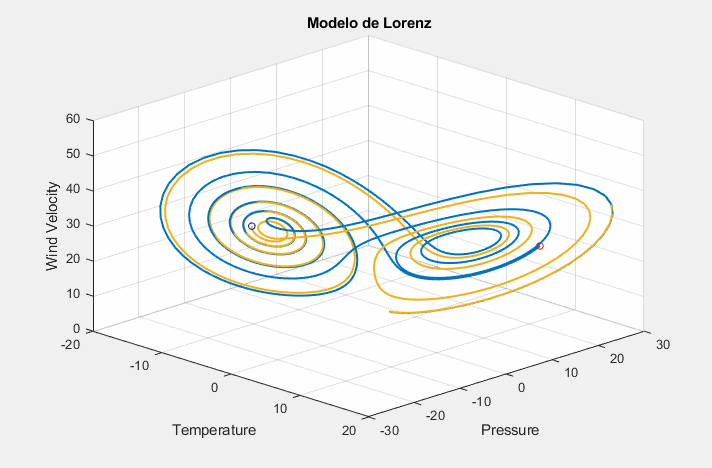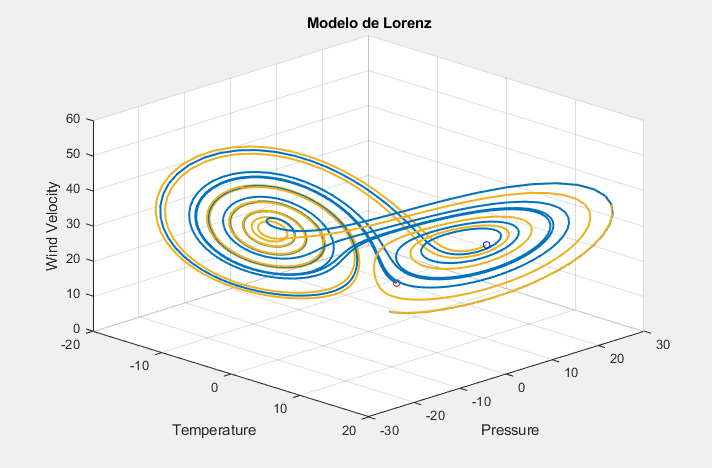
Objetivo principal
Aprender propriedades que os sinais obedecem quando passam por uma classe especial de sistemas:
Sistemas Lineares e Invariantes no Tempo (SLIT), causais, determinístico e não-caóticos.
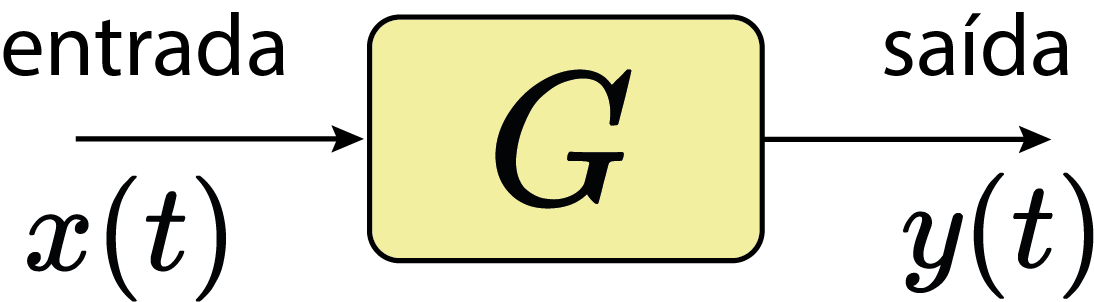
Sistemas Lineares Invariantes no Tempo (SLIT)
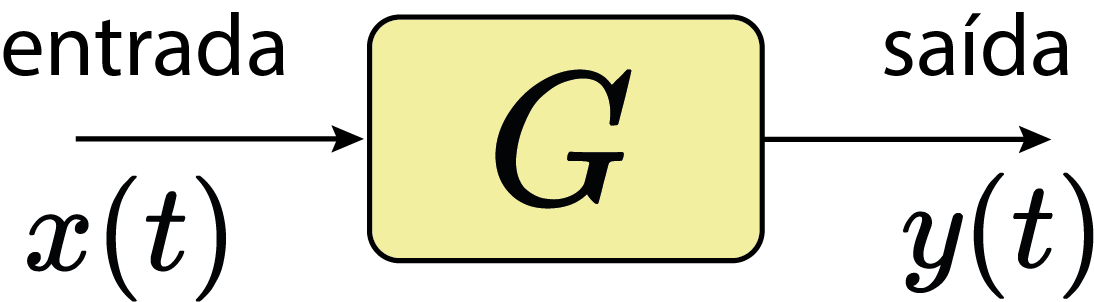
EDO Lineares: $$ \frac{d^n y}{dt^n}+\cdots+a_{n-1}\frac{dy}{dt}+a_ny=\frac{d^m x}{dt^m}+\cdots+b_{m-1}\frac{dx}{dt}+b_mx $$
Sistemas Lineares Invariantes no Tempo (SLIT)
Operador Derivadas: $$ Dy=\frac{dy}{dt},\quad D^2y =\frac{d^2y}{dt^2}, \quad \ldots $$
Sistemas Lineares Invariantes no Tempo (SLIT)
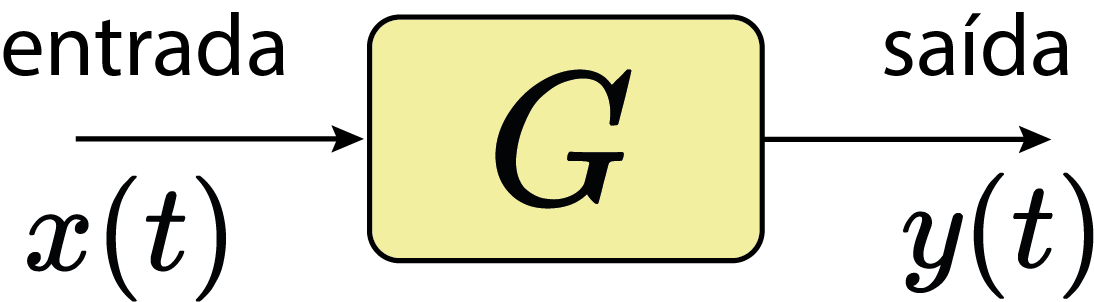
EDO Lineares: $$ D^n y+\cdots+a_{n-1}Dy+a_ny=D^m x+\cdots+b_{m-1}Dx+b_mx $$
Sistemas Lineares Invariantes no Tempo (SLIT)
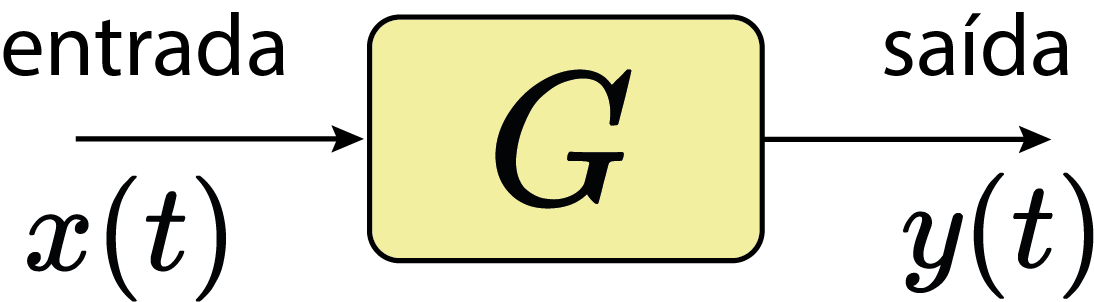
EDO Lineares: $$ (D^n +\cdots+a_{n-1}D+a_n)y=(D^m+\cdots+b_{m-1}D+b_m)x $$
Sistemas Lineares Invariantes no Tempo (SLIT)
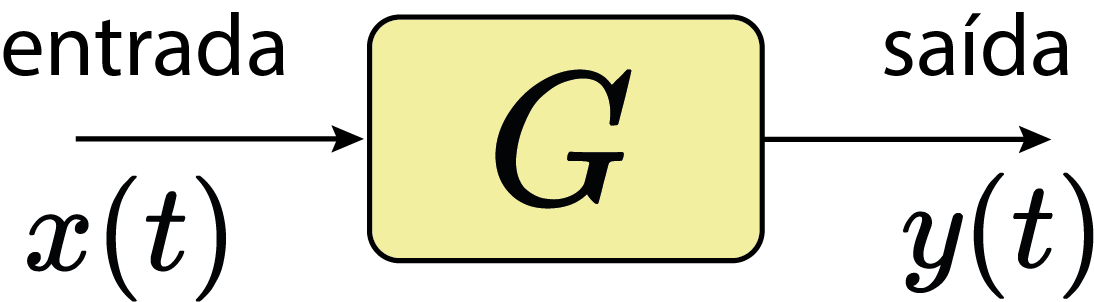
EDO Lineares: $$ P(D)y=N(D)x $$
Representação no tempo!Sistemas Lineares Invariantes no Tempo (SLIT)
EDO Lineares: $$ \frac{d^n y}{dt^n}+\cdots+a_{n-1}\frac{dy}{dt}+a_ny=\frac{d^m x}{dt^m}+\cdots+b_{m-1}\frac{dx}{dt}+b_mx $$
Sistemas Lineares Invariantes no Tempo (SLIT)
Equação Algébrica no plano complexo: $$ Y(\omega)=\underbrace{\frac{(j\omega)^m+\cdots+b_{m-1}j\omega+ b_m}{(j\omega)^n+\cdots+a_{n-1}j\omega+a_n}}_{G(\omega)}X(\omega) $$
Sistemas Lineares Invariantes no Tempo (SLIT)
Equação Algébrica no plano complexo: $$ Y(\omega)=G(\omega)X(\omega) $$
Sistemas Lineares Invariantes no Tempo (SLIT)
Sinal de Saída: $$ y(t)=g(t)\ast x(t) $$
Próxima aula
Modelagem de sistemas LIT.