

Aula 21:
Diagrama de Bode para SLIT
SEL0604
Prof. Marcos Rogério Fernandes
18 de novembro de 2024
Objetivos
Os objetivos dessa aula são entender:
- Componentes da função de transferência;
- Dinâmica de 1° e 2° ordem;
- Diagrama de Bode aproximado;
- Exemplos
Função de Transferência
Forma geral: $$ G(s)=\frac{Y(s)}{X(s)}=\frac{s^m+\cdots+b_{m-1}s+ b_m}{s^n+\cdots+a_{n-1}s+a_n} $$
Função de Transferência
Forma ZPK: $$ G(s)=K\frac{s+b}{s+a}\frac{(s+z)(s+z^*)}{(s+p)(s+p^*)} $$
FT=(ganho)+(zeros/polos reais) + (zeros/polos conjugados)Sistema estático
$$ G(s)=\frac{Y(s)}{X(s)}=K $$

Resistor ideal
Resposta em frequência
$$ G(j\omega)=\frac{Y(j\omega)}{X( j\omega)}=K $$
- Módulo?
- Fase?
Resposta do SLIT

Módulo $|G(j\omega)|$ = ganho do sistema na frequência $\omega$!
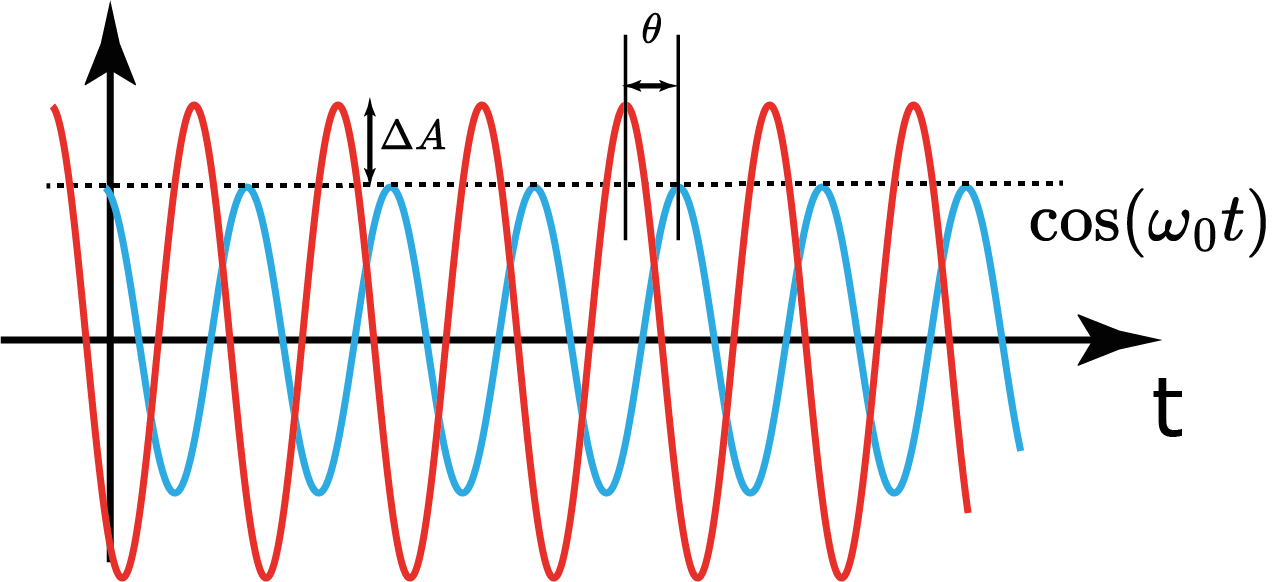
Escala Decibéis
$$ |G(j\omega)|_\text{dB}=20\log_{10}|G(j\omega)| $$
Propriedades de logaritmos: $$ \log_b(a)=x \Rightarrow b^x=a\\ \log_b(a_1a_2)=\log_b(a_1)+\log_b(a_2)\\ \log_b(\frac{1}{a})=\log_b(a^{-1})=-\log_b(a) $$Escala Absoluta
$$ |G(j\omega)|=10^{\frac{1}{20}|G(j\omega)|_\text{dB}} $$
Propriedades de logaritmos: $$ \log_b(a)=x \Rightarrow b^x=a\\ \log_b(a_1a_2)=\log_b(a_1)+\log_b(a_2)\\ \log_b(\frac{1}{a})=\log_b(a^{-1})=-\log_b(a) $$Resposta em frequência
$$ G(j\omega)=\frac{Y(j\omega)}{X( j\omega)}=K $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Resposta em frequência

Resposta em frequência

Dinâmica de 1° Ordem
$$ G(s)=\frac{Y(s)}{X(s)}=\frac{1}{s+a} $$
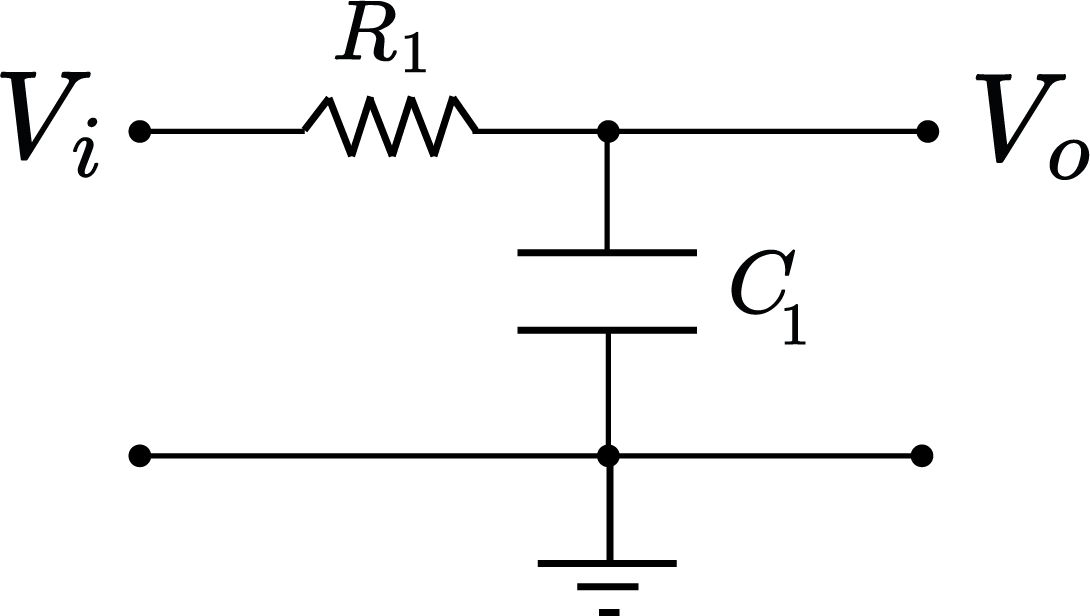
Circuito RC
Resposta em frequência
$$ G(j\omega)=\frac{Y(j\omega)}{X(j\omega)}=\frac{1}{j\omega+a} $$
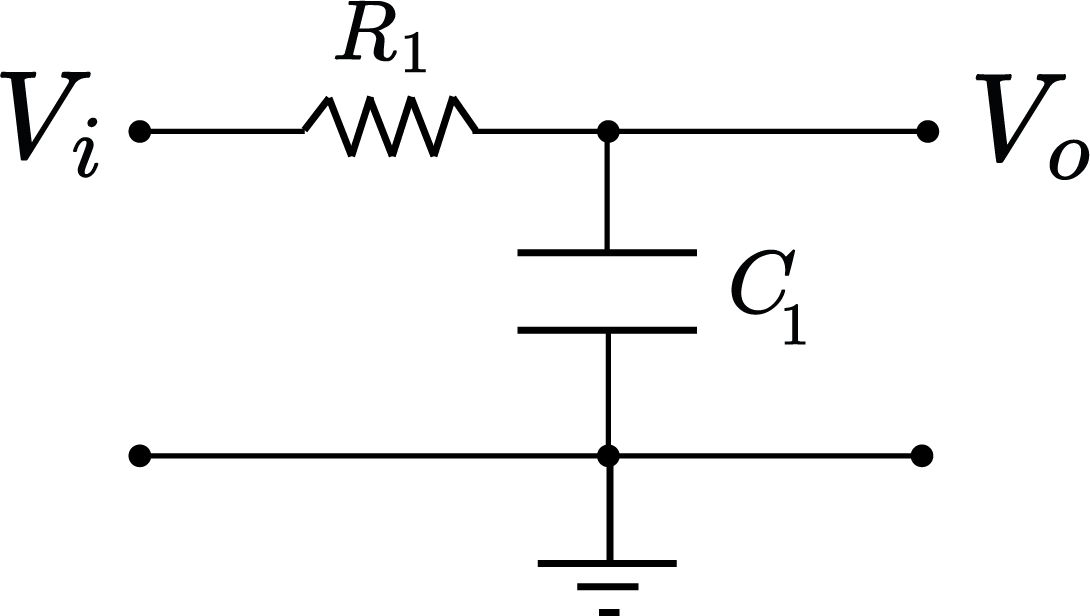
Circuito RC
Resposta em frequência
$$ G(j\omega)=\frac{Y(j\omega)}{X(j\omega)}=\frac{\frac{1}{a}}{j\frac{\omega}{a}+1} $$
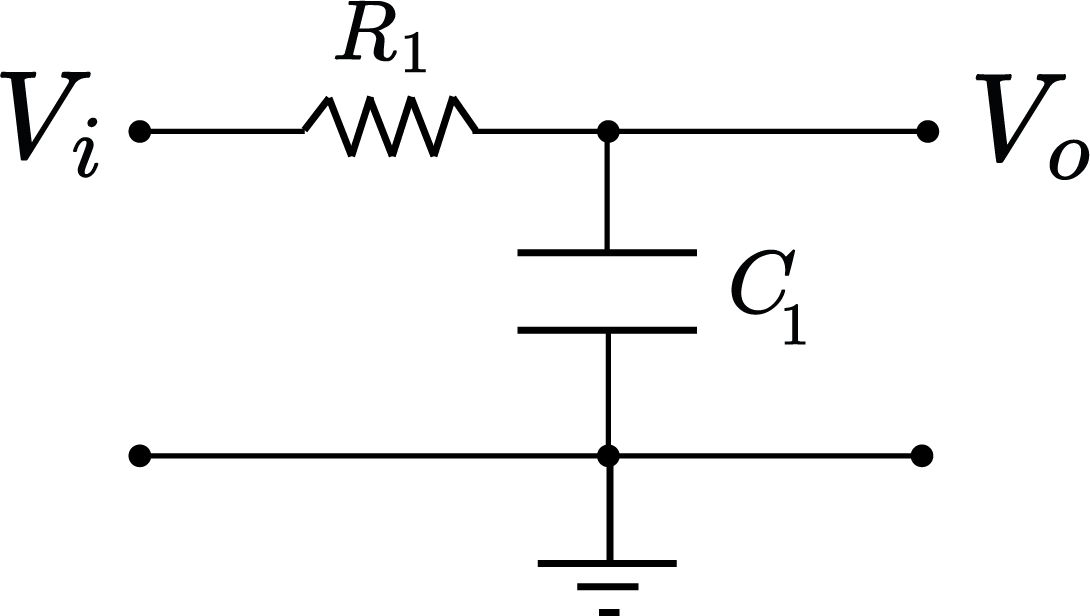
Circuito RC
Resposta em frequência
$$ G(j\omega)=\frac{Y(j\omega)}{X(j\omega)}=\frac{1}{j\frac{\omega}{a}+1} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Resposta em frequência
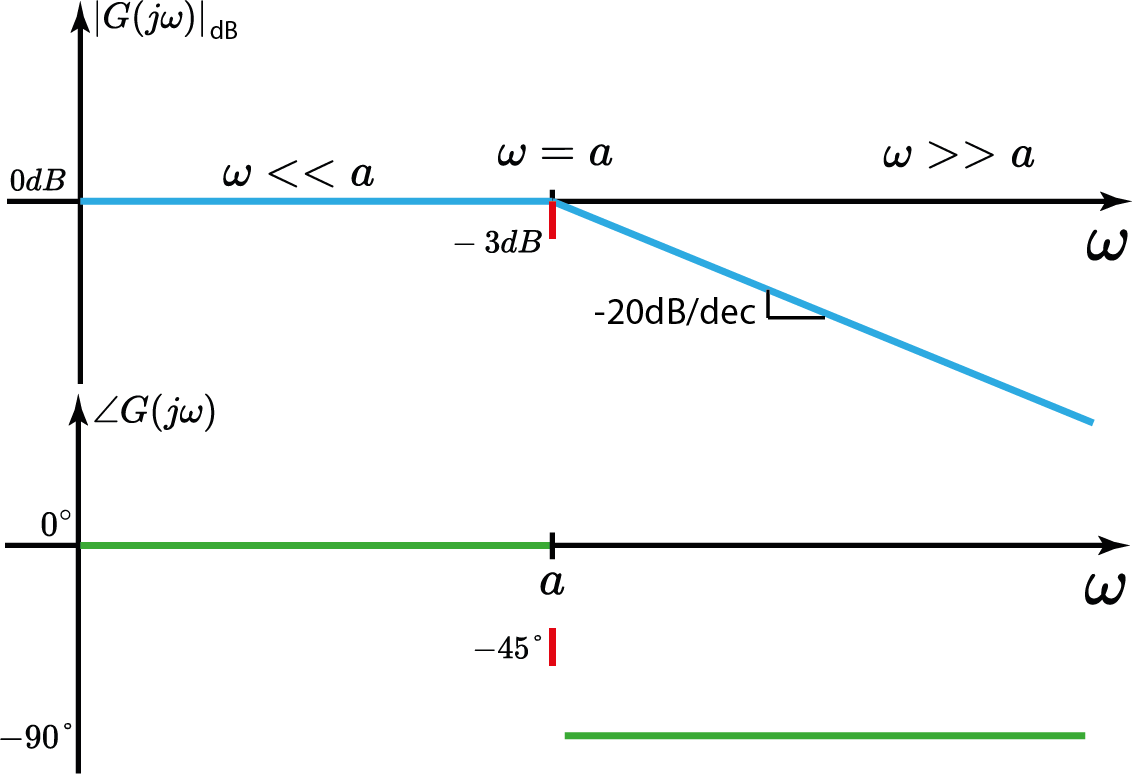
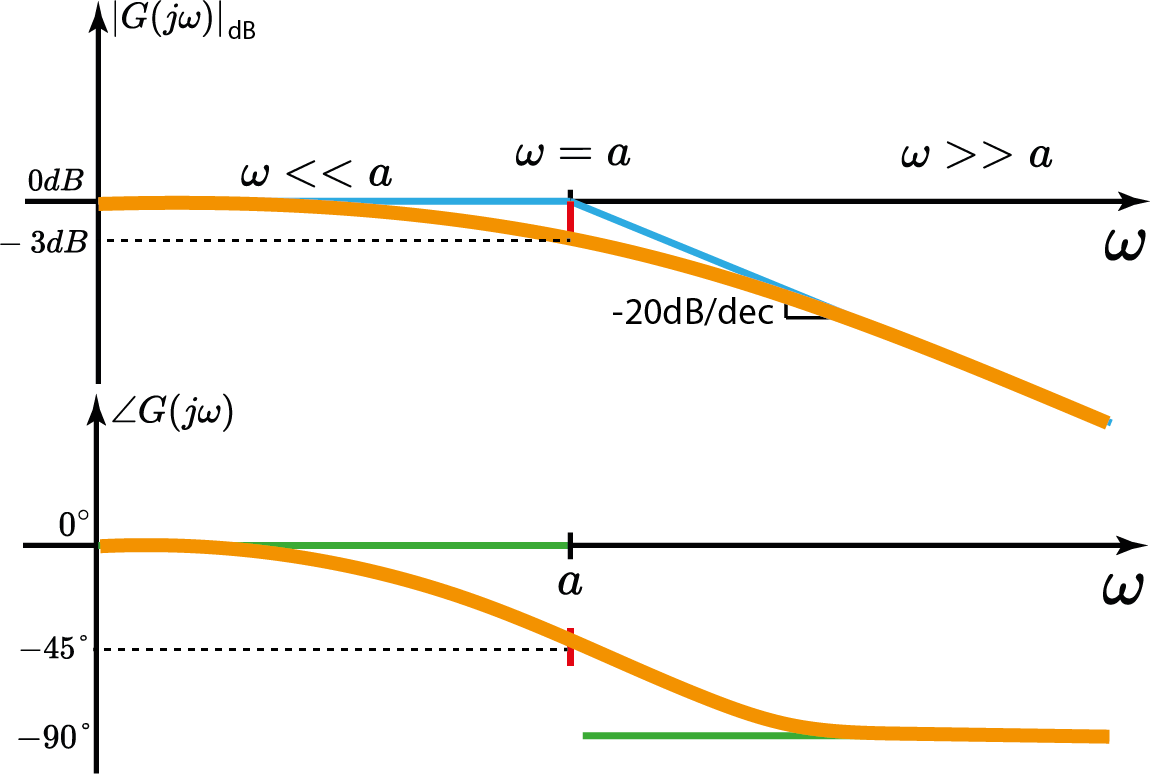
$$ |G(j\omega)|_{dB}=-20\log_{10}|j\frac{\omega}{a}+1| $$
- 1° caso: $\omega < < a$
- 2° caso: $\omega > > a$
- 3° caso: $\omega=a$
Resposta em frequência
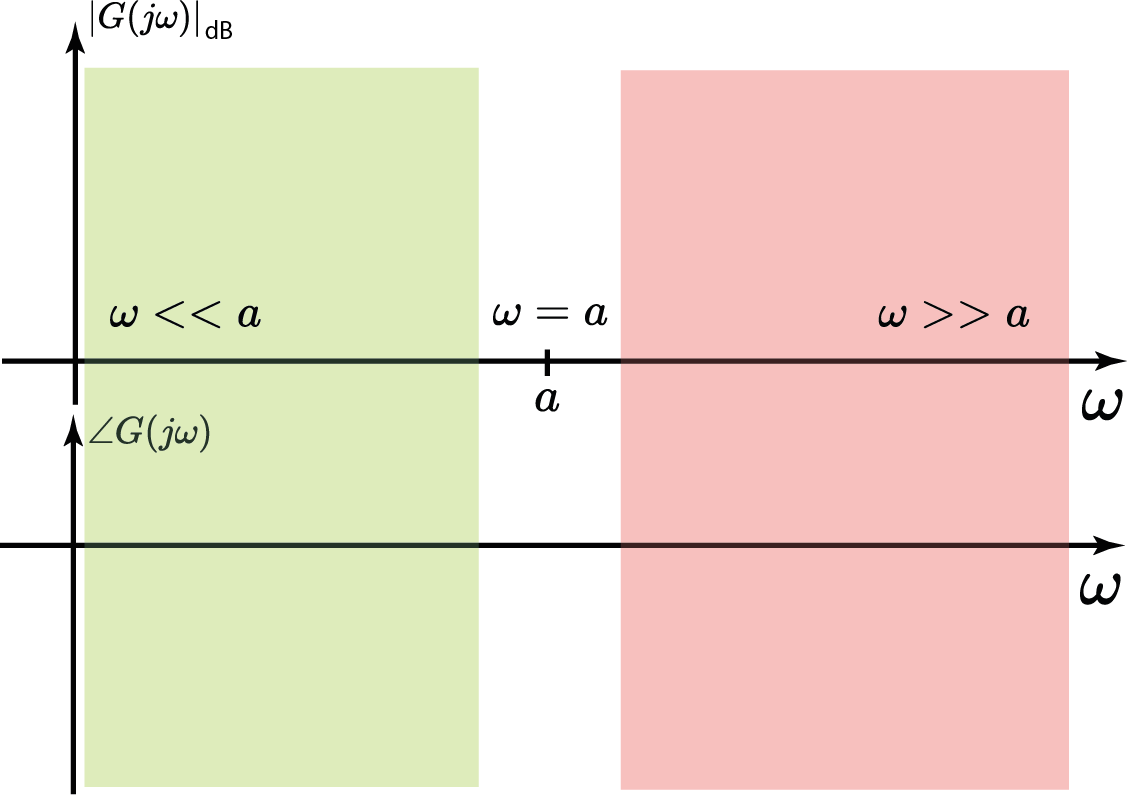
Resposta em frequência
1° caso: $\omega < < a$ $$ |G(j\omega)|_{dB}\approxeq-20\log_{10}|1|=0dB $$
O sistema tem ganho aproximadamente unitário em baixas frequências!1° caso: $\omega < < a$ $$ \angle G(j\omega)\approxeq \angle 1=0° $$
Resposta em frequência

Resposta em frequência
2° caso: $\omega > > a$ $$ |G(j\omega)|_{dB}\approxeq-20\log_{10}\Bigl|\frac{\omega}{a}\Bigl| $$
2° caso: $\omega > > a$ $$ \angle G(j\omega)\approxeq\angle -j\frac{a}{\omega}=-90° $$
Resposta em frequência
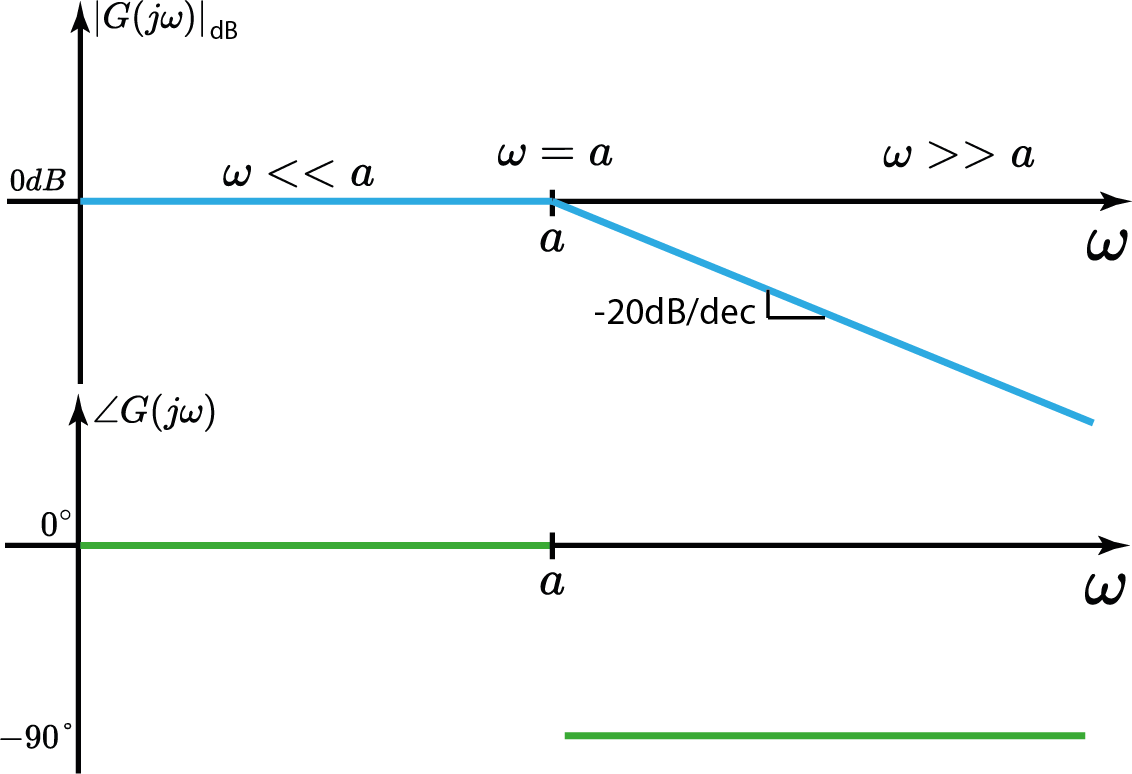
Resposta em frequência
3° caso: $\omega=a$ $$ |G(j\omega)|_{dB}=-20\log_{10}\sqrt{2}\approxeq -3dB $$
3° caso: $\omega > > a$ $$ \angle G(j\omega)=\angle \frac{1}{1+j}=-45° $$
Resposta em frequência
Resposta em frequência
Sistema c/ 2 pólos reais
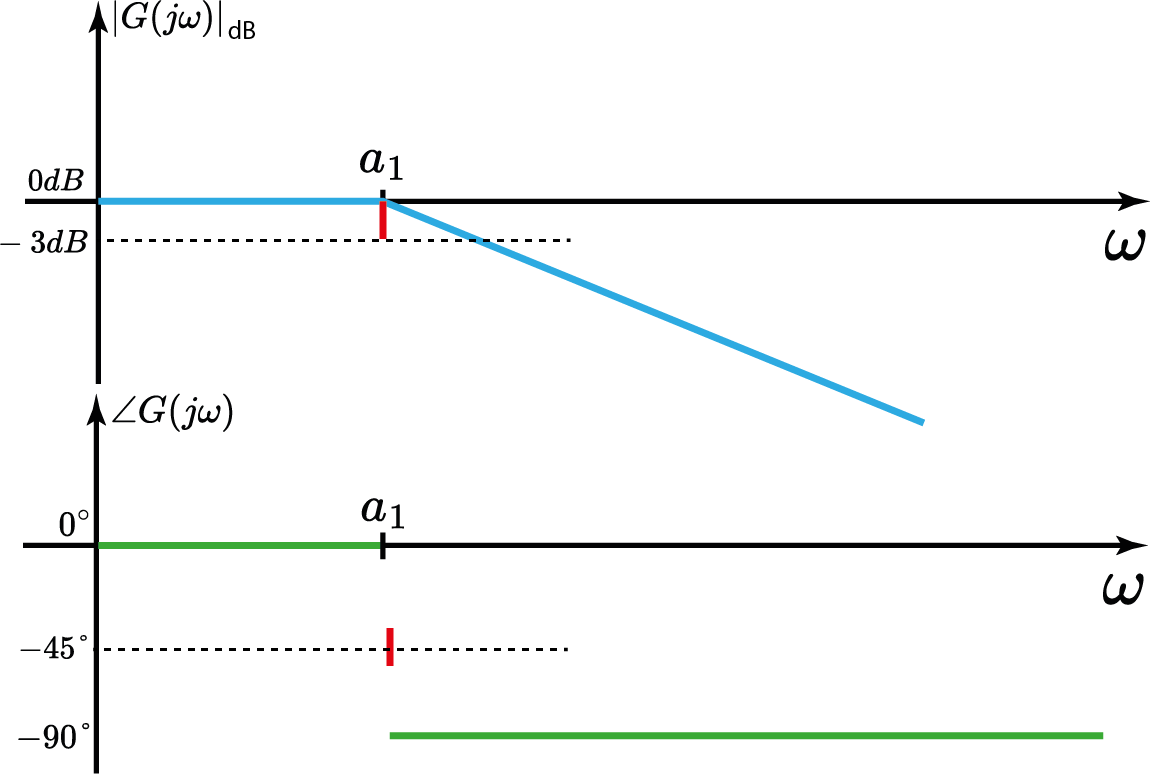
$$ G(s)=\frac{Y(s)}{X(s)}=\frac{1}{(s+a_1)(s+a_2)} $$ com $a_1< a_2$.
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ 2 pólos reais
$$ G(j\omega )=\frac{1}{(j\omega+a_1)(j\omega+a_2)} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ 2 pólos reais
$$ G(j\omega )=\frac{\frac{1}{a_1a_2}}{(j\frac{\omega}{a_1}+1)(j\frac{\omega}{a_2}+1)} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ 2 pólos reais
$$ G(j\omega )=\frac{1}{(j\frac{\omega}{a_1}+1)(j\frac{\omega}{a_2}+1)} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ 2 pólos reais
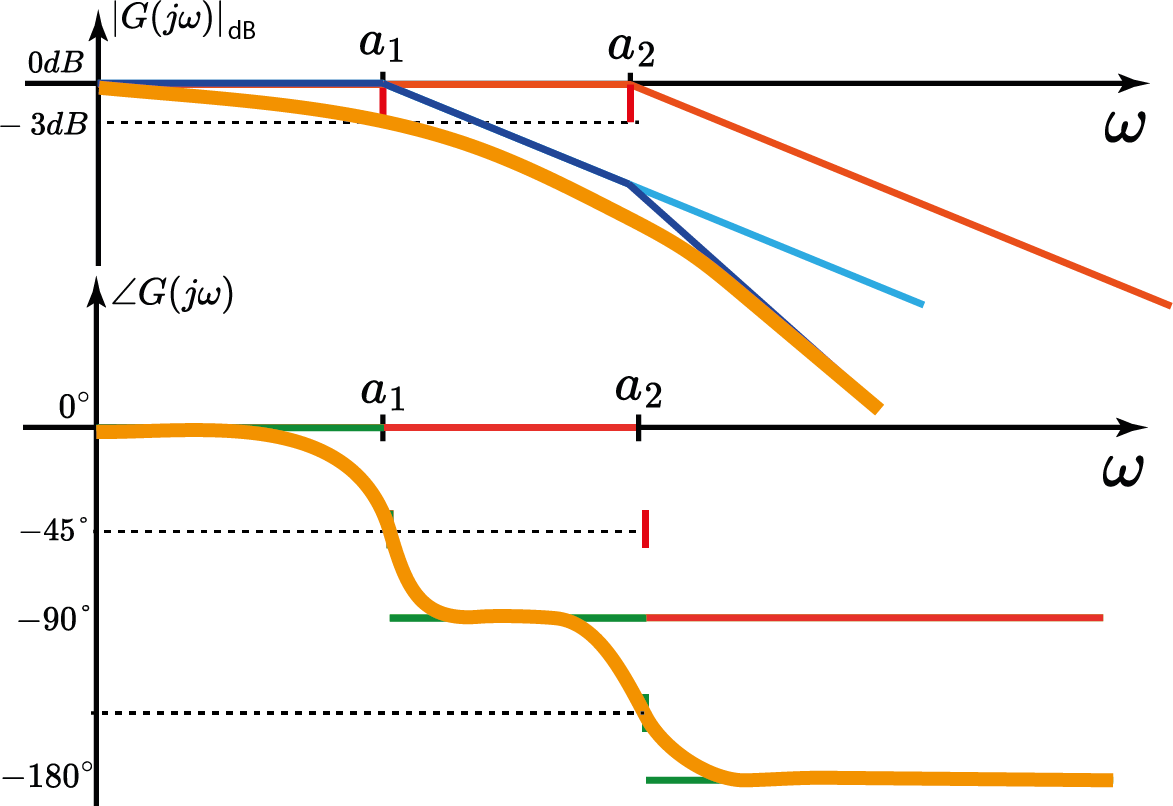
Sistema c/ 2 pólos reais
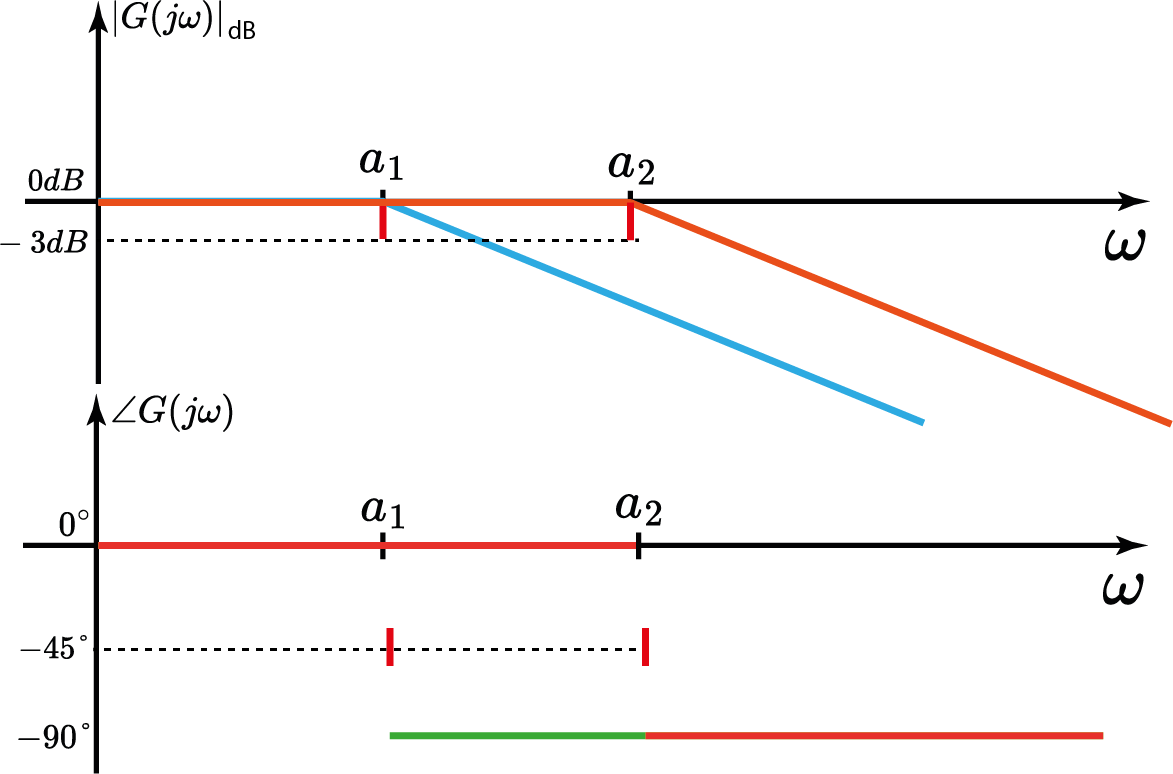
Sistema c/ 2 pólos reais
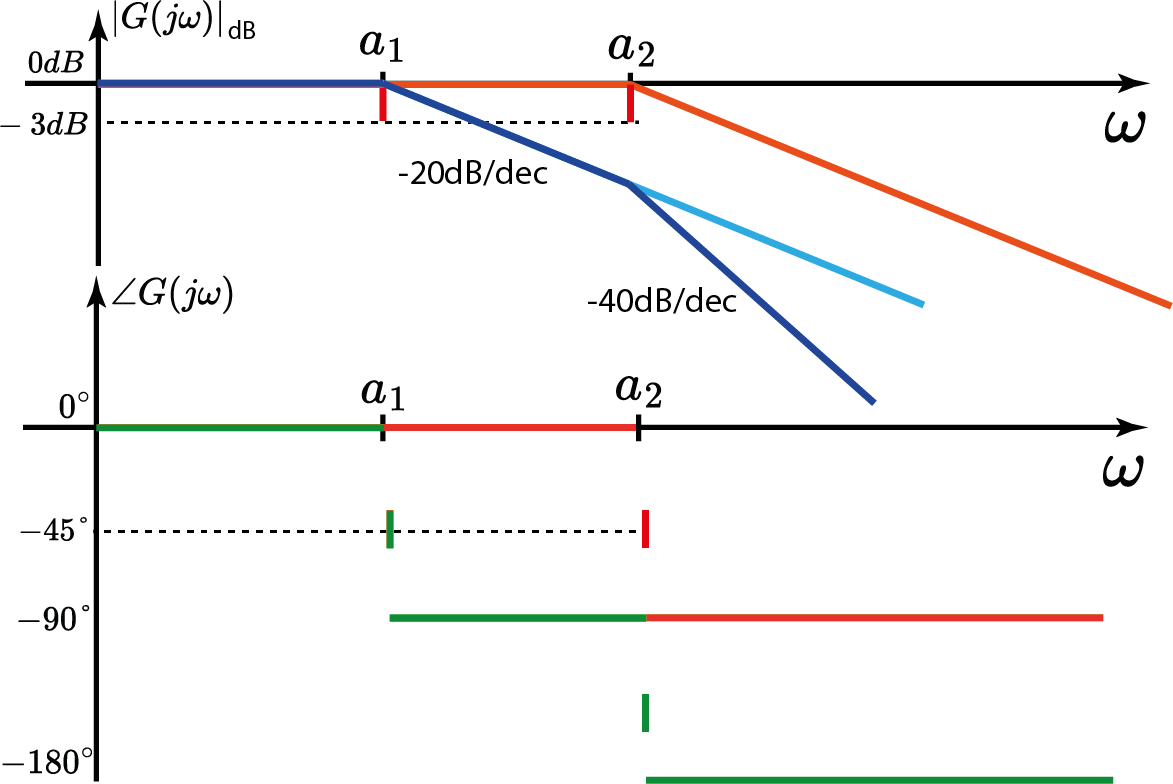
Sistema c/ 2 pólos reais
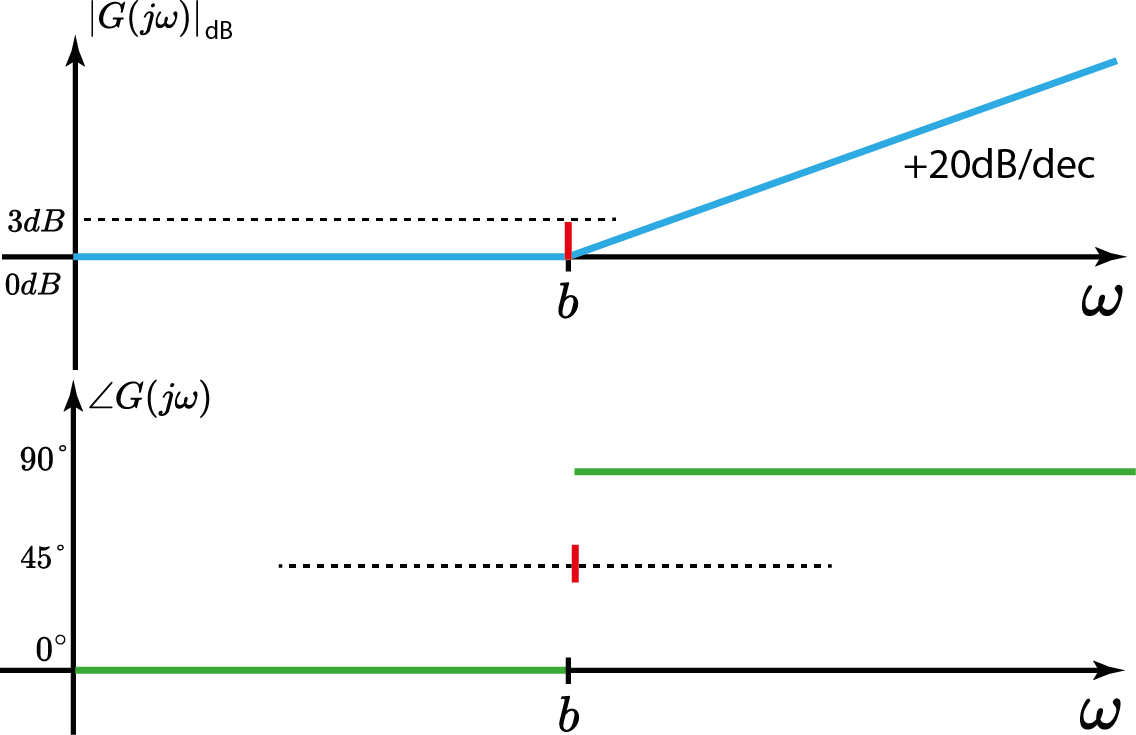
Sistema c/ zero real
$$ G(s)=\frac{Y(s)}{X(s)}=s+b=\frac{1}{(s+b)^{-1}} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
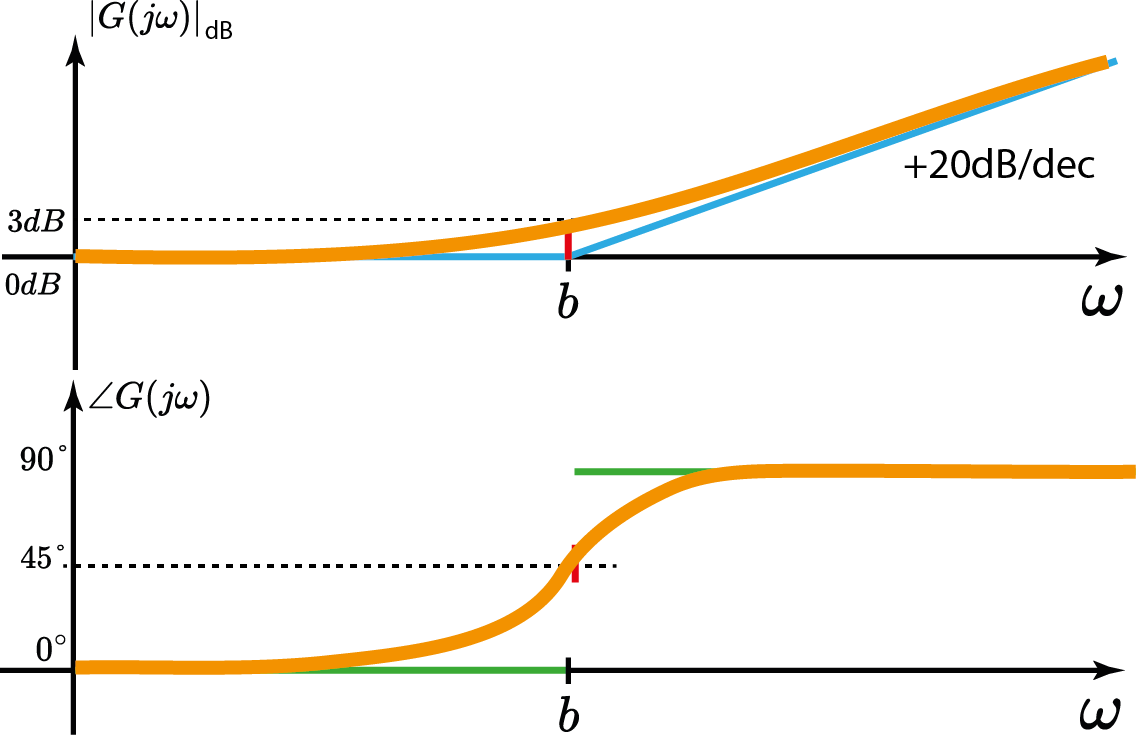
Sistema c/ zero real
Sistema c/ zero real
Sistema c/ pólo na origem
$$ G(s)=\frac{Y(s)}{X(s)}=\frac{1}{s} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ pólo na origem
$$ G(j\omega)=\frac{1}{j\omega} $$
$$ |G(j\omega)|_{dB}=-20\log_{10}|\omega|\\ \angle G(j\omega)=-90° $$Sistema c/ pólo na origem
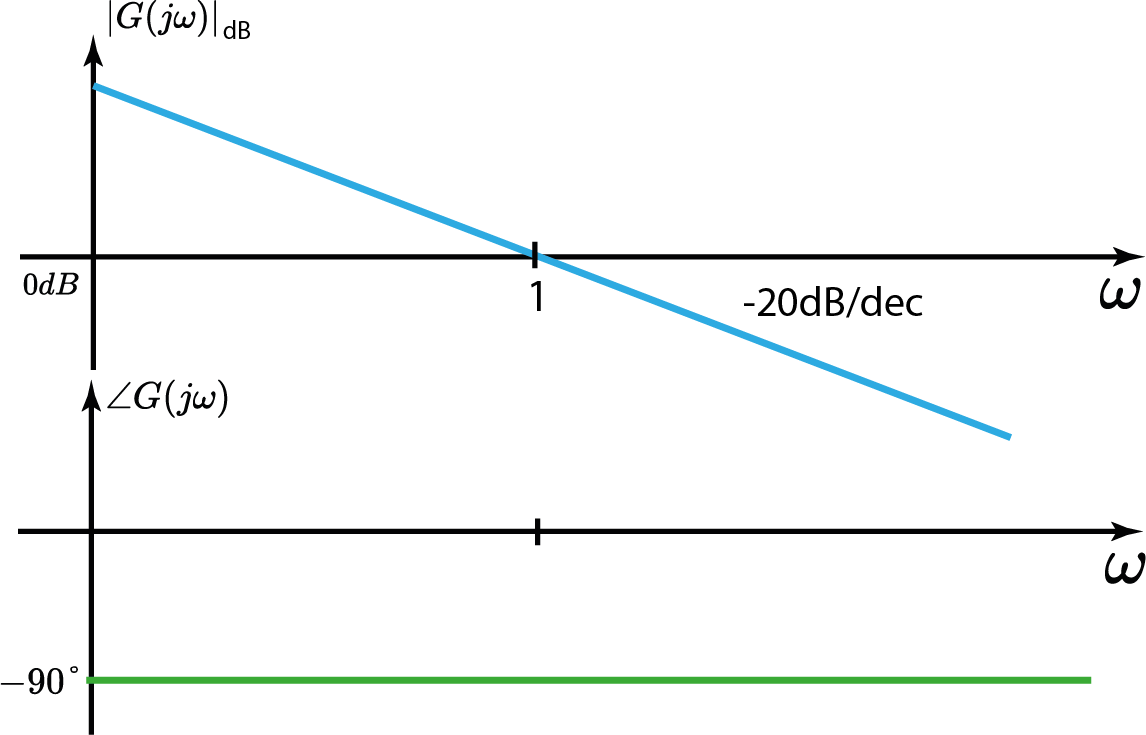
Sistema c/ zero na origem
$$ G(j\omega)=j\omega $$
$$ |G(j\omega)|_{dB}=+20\log_{10}|\omega|\\ \angle G(j\omega)=+90° $$Sistema c/ zero na origem
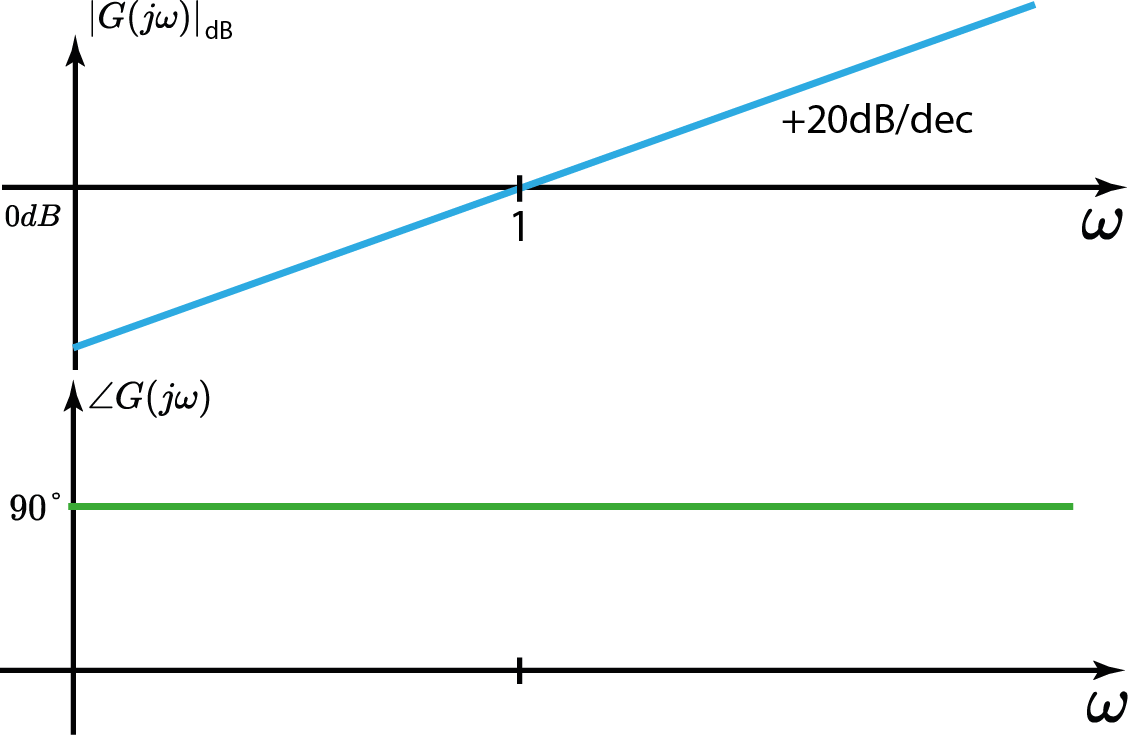
Dinâmica de 2° Ordem
$$ G(s)=\frac{Y(s)}{X(s)}=\frac{1}{(s+p)(s+p^*)} $$
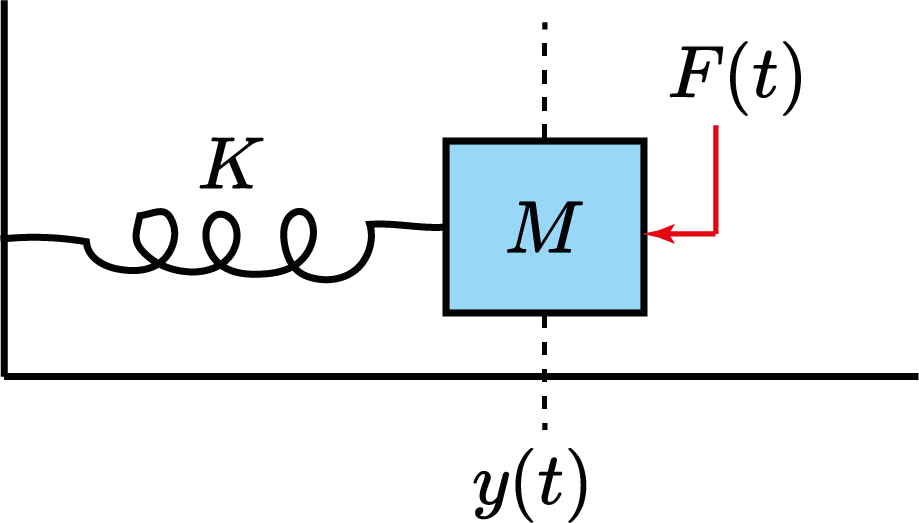
Massa-Mola
Sistema de 2° Ordem
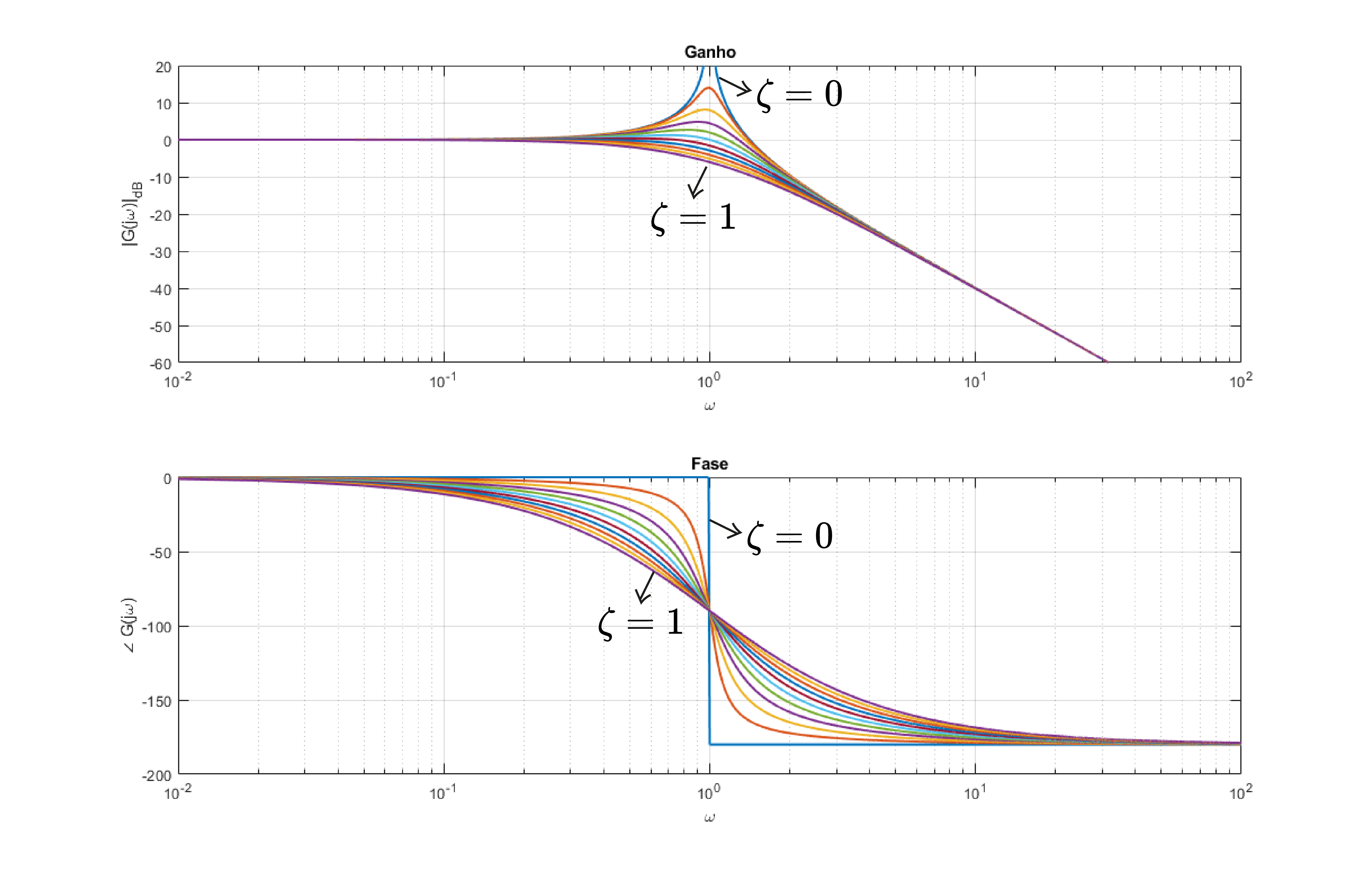
Forma padrão: $$ G(s)=\frac{Y(s)}{X(s)}=\frac{\omega_n^2}{s^2+2\zeta\omega_n s +\omega_n^2} $$
Seja $p=a+jb$, então $$ \omega_n=\sqrt{a^2+b^2}\to \text{frequência natural}\\ \zeta=\frac{a}{\sqrt{a^2+b^2}} \to \text{coef. de amortecimento} $$Sistema de 2° Ordem
$$ G(s)=\frac{Y(s)}{X(s)}=\frac{1}{(\frac{s}{\omega_n})^2+2\zeta(\frac{s}{\omega_n}) +1} $$
Seja $p=a+jb$, então $$ \omega_n=\sqrt{a^2+b^2}\\ \zeta=\frac{a}{\sqrt{a^2+b^2}},\quad 0\le \zeta \le 1 $$Sistema de 2° Ordem
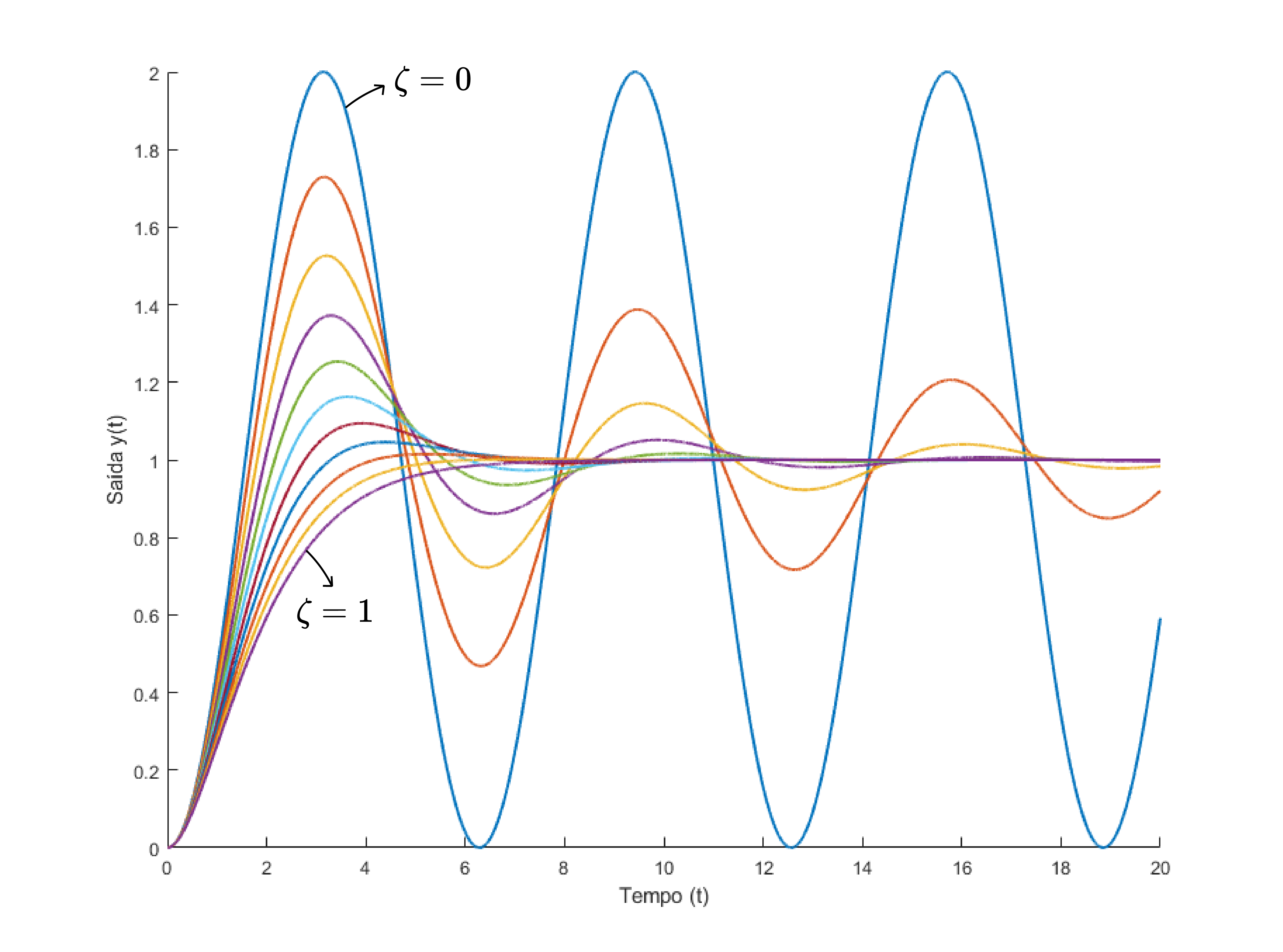
Sistema de 2° Ordem
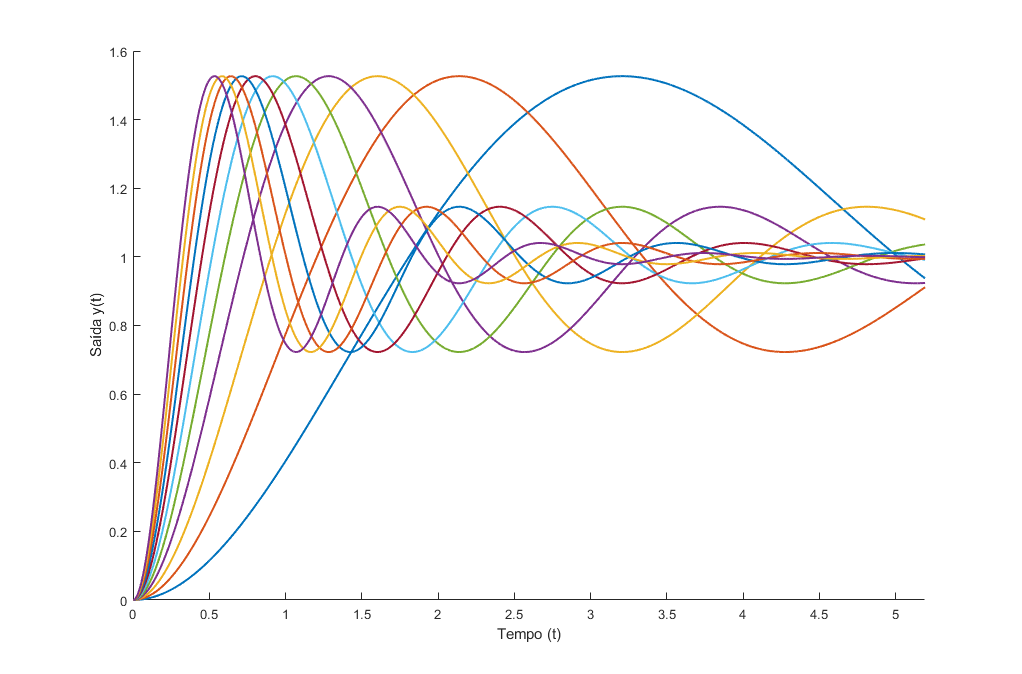
Sistema de 2° Ordem
$$ G(j\omega)=\frac{1}{(\frac{j\omega}{\omega_n})^2+2\zeta(\frac{j\omega}{\omega_n}) +1} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema de 2° Ordem
$$ |G(j\omega)|_{dB}=-20\log_{10}\Bigl|(\frac{j\omega}{\omega_n})^2+2\zeta(\frac{j\omega}{\omega_n}) +1\Bigr| $$
- 1° caso: $\omega < < \omega_n$
- 2° caso: $\omega > > \omega_n$
- 3° caso: $\omega=\omega_n$
Sistema de 2° Ordem
1° caso: $\omega < < \omega_n$ $$ |G(j\omega)|_{dB}\approxeq-20\log_{10}|1|=0dB $$
1° caso: $\omega < < \omega_n$ $$ \angle G(j\omega)\approxeq\angle 1=0° $$
Sistema de 2° Ordem

Sistema de 2° Ordem
2° caso: $\omega > > \omega_n$ $$ |G(j\omega)|_{dB}\approxeq-40\log_{10}\Bigl|\frac{\omega}{\omega_n}\Bigr| $$
2° caso: $\omega > >\omega_n$ $$ \angle G(j\omega)\approxeq -180° $$
Sistema de 2° Ordem
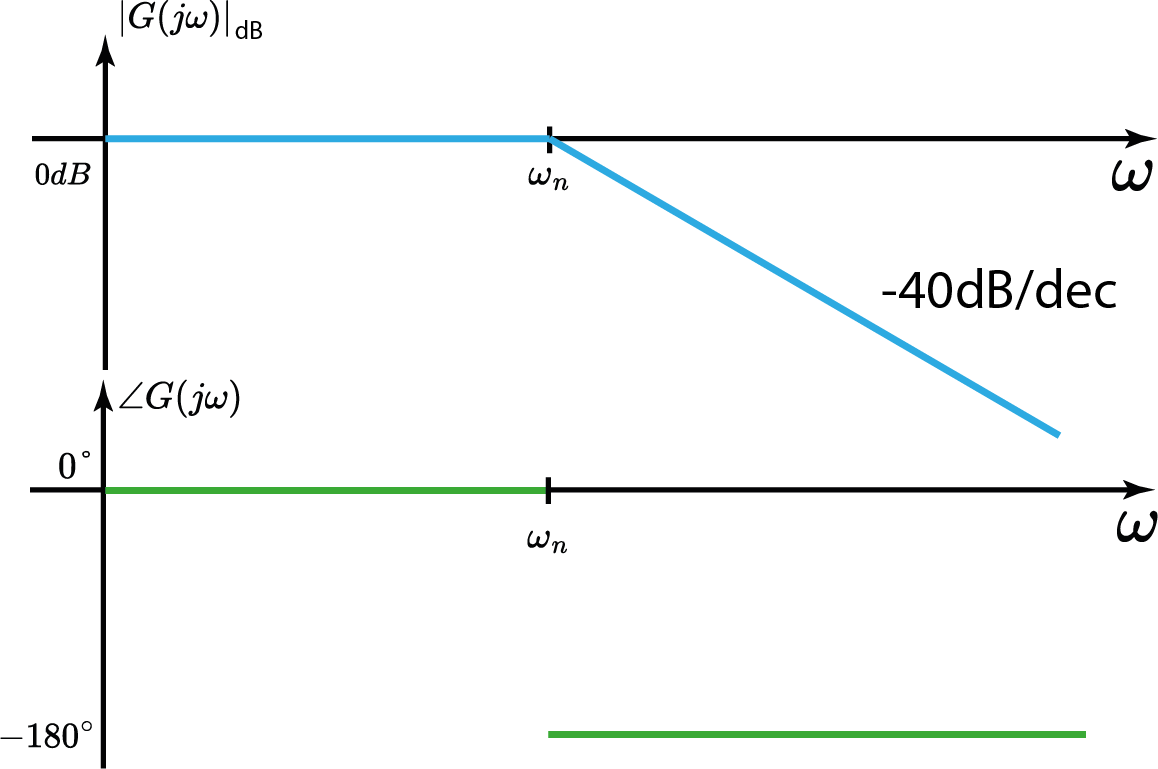
Sistema de 2° Ordem
3° caso: $\omega = \omega_n$ $$ |G(j\omega)|_{dB}=-20\log_{10}|2\zeta| $$
3° caso: $\omega = \omega_n$ $$ \angle G(j\omega)=-90° $$
Sistema de 2° Ordem
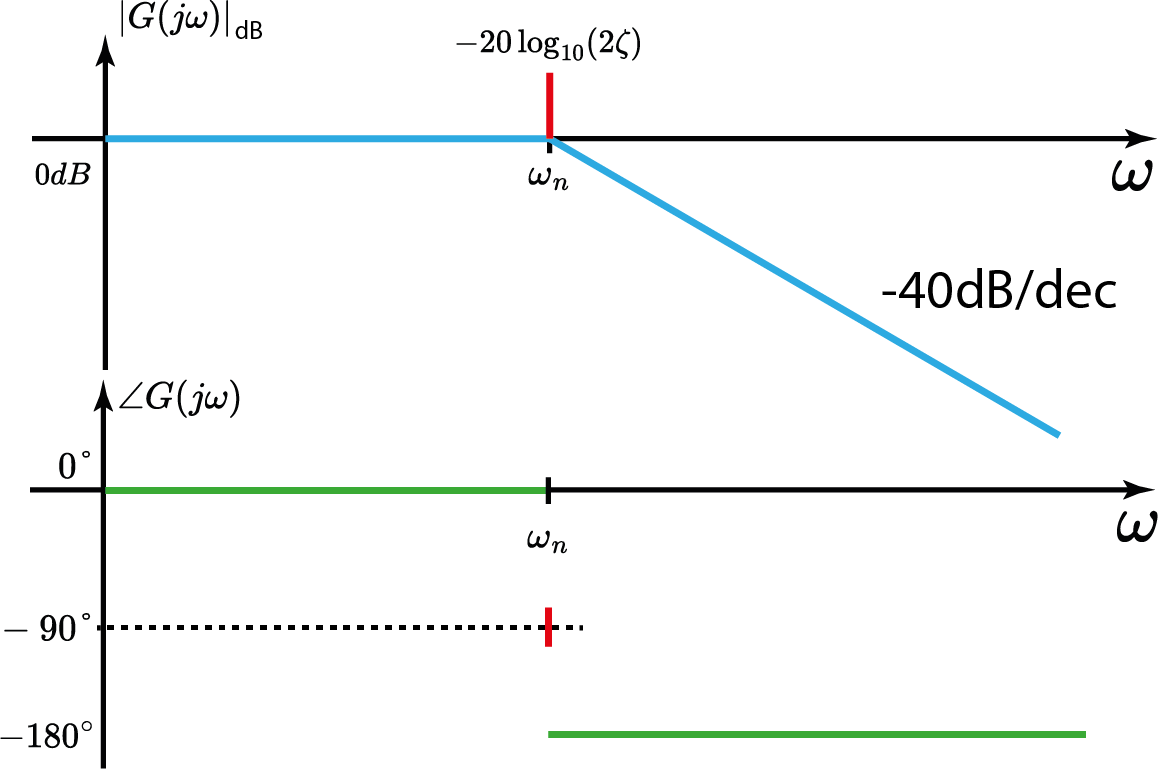
Sistema de 2° Ordem
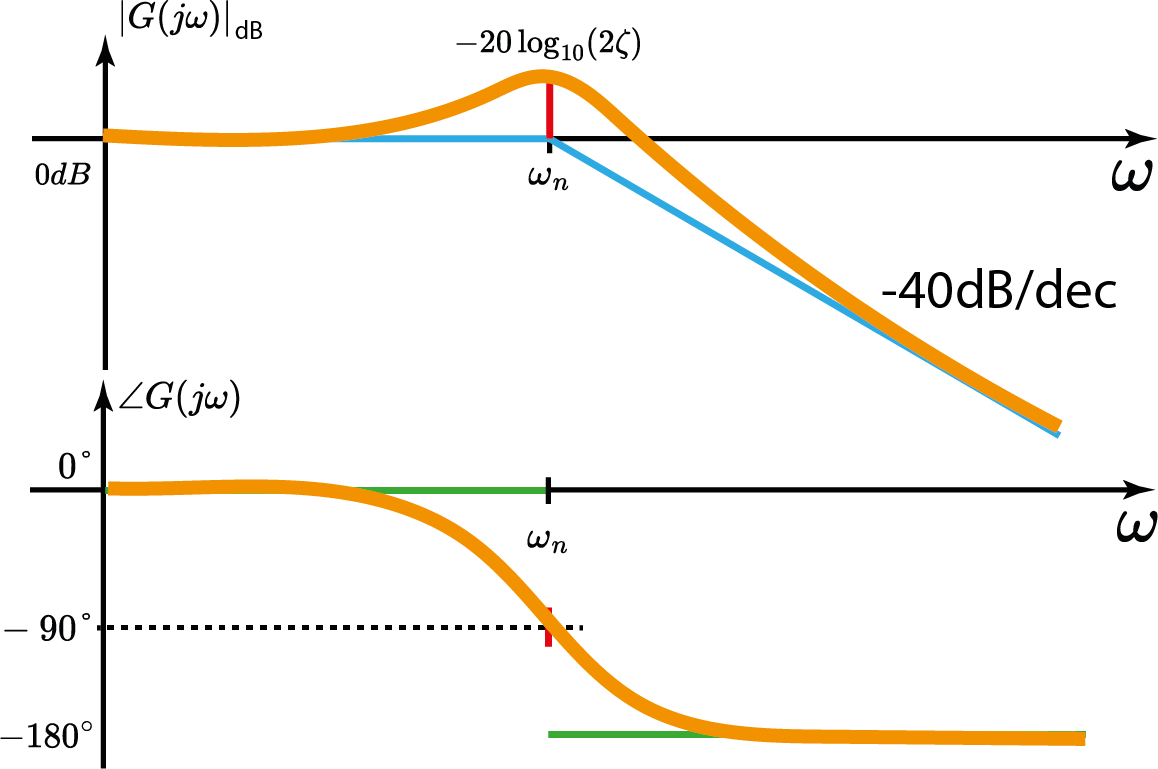
Sistema de 2° Ordem
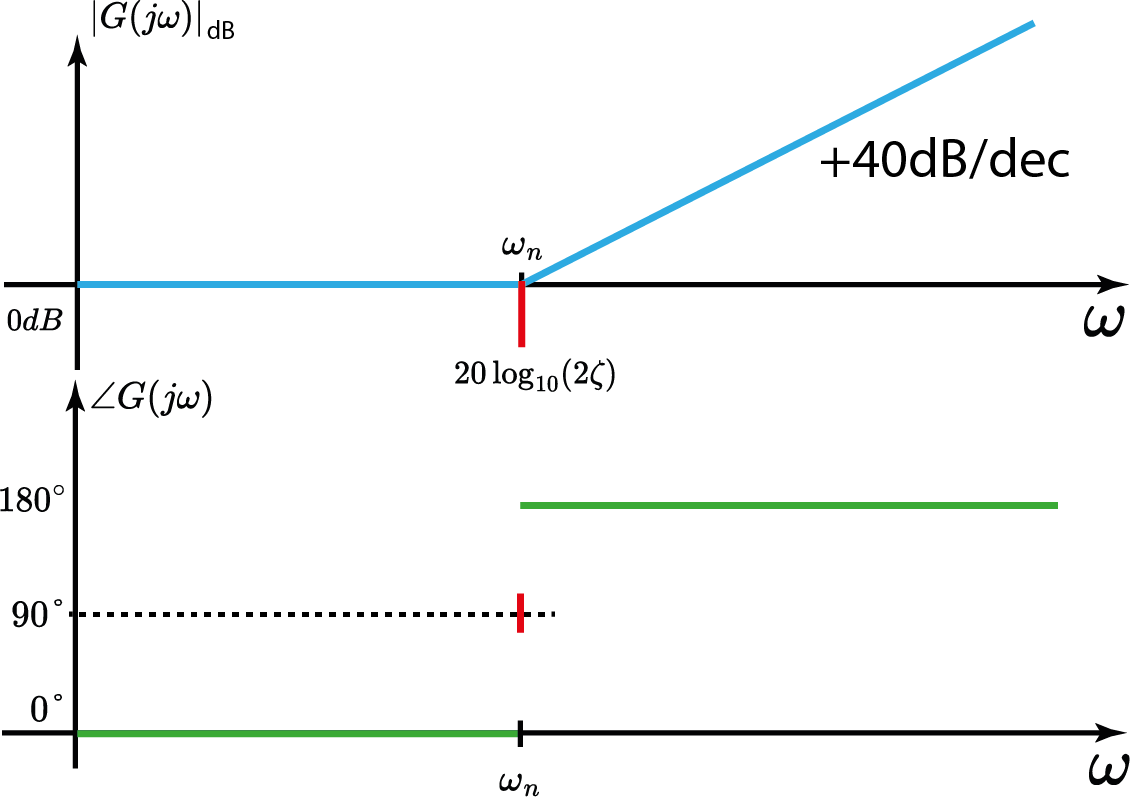
Sistema c/ zeros conjugados
$$ G(j\omega)=\frac{1}{((\frac{j\omega}{\omega_n})^2+2\zeta(\frac{j\omega}{\omega_n}) +1)^{-1}} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Sistema c/ zeros conjugados
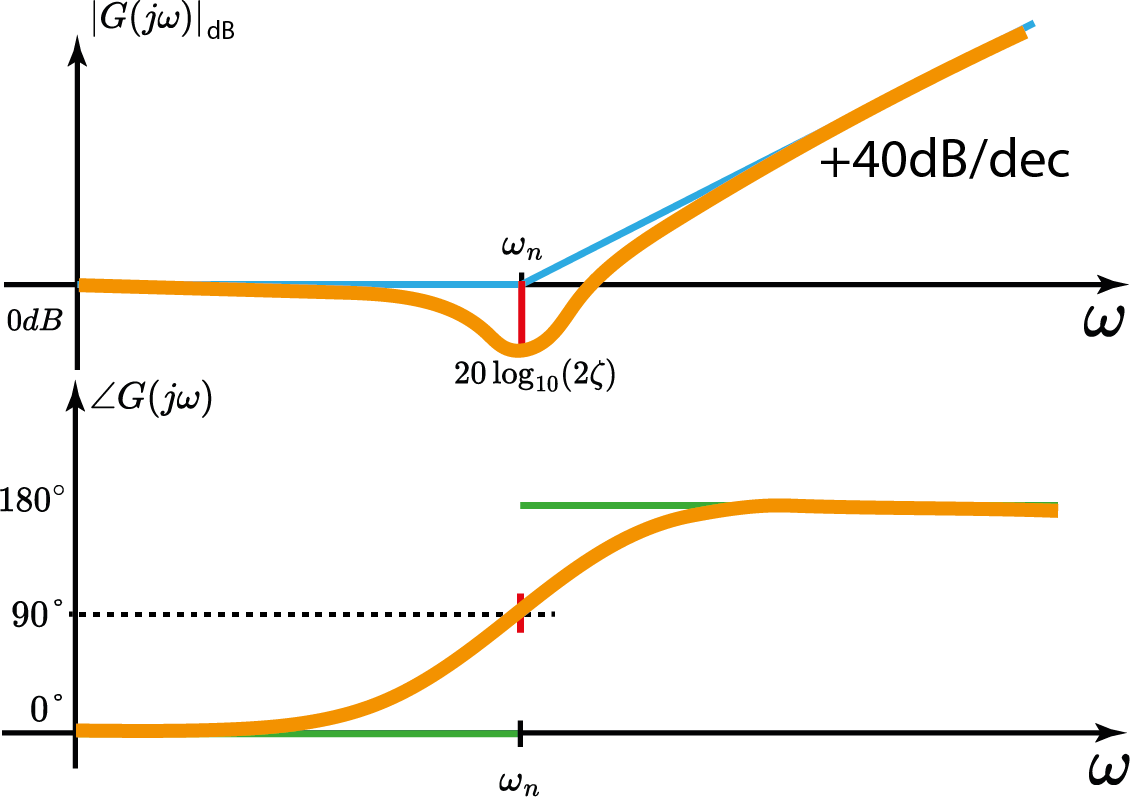
$$ |G(j\omega)|_{dB}=+20\log_{10}\Bigl|(\frac{j\omega}{\omega_n})^2+2\zeta(\frac{j\omega}{\omega_n}) +1\Bigr| $$
- 1° caso: $\omega < < \omega_n$
- 2° caso: $\omega > > \omega_n$
- 3° caso: $\omega=\omega_n$
Sistema c/ zeros conjugados
Sistema c/ zeros conjugados
Exemplo:
$$ G(s)=5\frac{s+1}{s+2}\frac{1}{s^2+2s+4} $$
- Qual o ganho do sistema em dB em função de $\omega$?
- Qual a fase do sistema em função de $\omega$?
Próxima aula
Diagrama de Blocos para SLIT